L'Hopital's Rule, College Calculus: Level I

Loading video...

Next Lecture

Previous Lecture

Discussion
Quick Notes
Download Lecture Slides
Table of Contents
Related Books

Please login to ask a question and view discussion.

Start Learning Now

Our free lessons will get you started (Flash® 10 required).
Get immediate access to our entire library.

Features Overview

Get on-demand access to our complete library
Search and jump to exactly what you need to learn
Track your progress
Download practice and lesson files
*Ask questions and get answers from our community & instructors

L'Hopital's Rule

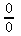Start by checking to see if you are dealing with an indeterminate type of limit of the form or 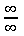. If so, proceed with L’Hopital’s Rule.
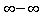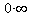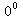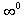Remember that it may be necessary to use L’Hopital’s Rule more than once!
If your limit is of another indeterminate type such as , , , , or 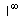, then you can rearrange the problem into a L’Hopital’s Rule form.
If your limit is not indeterminate at all, then simply complete the limit computation by ordinary methods!

L'Hopital's Rule

Lecture Slides are screen-captured images of important points in the lecture. Students can download and print out these lecture slide images to do practice problems as well as take notes while watching the lecture.

Intro

Using L'Hopital's Rule

Informal Definition

Lecture Example 1

Lecture Example 2

Lecture Example 3

Lecture Example 4

Additional Example 5

Additional Example 6

I. Overview of Functions
	Review of Functions	26:29
	Compositions of Functions	12:29
II. Limits
	Average and Instantaneous Rates of Change	20:59
	Limit Investigations	22:37
	Algebraic Evaluation of Limits	28:19
	Formal Definition of a Limit	23:39
	Continuity and the Intermediate Value Theorem	19:09
III. Derivatives, part 1
	Limit Definition of the Derivative	22:52
	The Power Rule	26:01
	The Product Rule	14:54
	The Quotient Rule	19:17
	Applications of Rates of Change	17:43
	Trigonometric Derivatives	26:58
	The Chain Rule	23:47
	Inverse Trigonometric Functions	27:05
	Equation of a Tangent Line	15:52
IV. Derivatives, part 2
	Implicit Differentiation	30:05
	Higher Derivatives	13:16
	Logarithmic and Exponential Function Derivatives	17:42
	Hyperbolic Trigonometric Function Derivatives	14:30
	Related Rates	29:05
	Linear Approximation	23:52
V. Application of Derivatives
	Absolute Minima and Maxima	18:57
	Mean Value Theorem and Rolle's Theorem	20:00
	First Derivative Test, Second Derivative Test	27:11
	L'Hopital's Rule	23:09
	Curve Sketching	40:16
	Applied Optimization	25:37
	Newton's Method	25:13
VI. Integrals
	Approximating Areas and Distances	36:50
	Riemann Sums, Definite Integrals, Fundamental Theorem of Calculus	22:02
	Substitution Method for Integration	23:19
VII. Application of Integrals, part 1
	Area Between Curves	19:59
	Volume by Method of Disks and Washers	24:22
	Volume by Method of Cylindrical Shells	30:29
	Average Value of a Function	16:31
VIII. Extra
	Graphs of f, f', f''	23:58
	Slope Fields for Differential Equations	18:32
	Separable Differential Equations	17:04

Mathematics: College Calculus: Level I

I. Overview of Functions
	Review of Functions			26:29
		Intro		0:00
		What is a Function		0:10
			Domain and Range	0:21
			Vertical Line Test	0:31
			Example: Vertical Line Test	0:47
		Function Examples		1:57
			Example: Squared	2:10
			Example: Natural Log	2:41
			Example: Exponential	3:21
			Example: Not Function	3:54
		Odd and Even Functions		4:39
			Example: Even Function	5:10
			Example: Odd Function	5:53
		Odd and Even Examples		6:48
			Odd Function	6:55
			Even Function	8:43
		Increasing and Decreasing Functions		10:15
			Example: Increasing	10:42
			Example: Decreasing	10:55
		Increasing and Decreasing Examples		11:41
			Example: Increasing	11:48
			Example: Decreasing	12:33
		Types of Functions		13:32
			Polynomials	13:45
			Powers	14:06
			Trigonometric	14:34
			Rational	14:50
			Exponential	15:13
			Logarithmic	15:29
		Lecture Example 1		15:55
		Lecture Example 2		17:51
		Additional Example 3		2:35
		Additional Example 4		2:33
	Compositions of Functions			12:29
		Intro		0:00
		Compositions		0:09
			Alternative Notation	0:32
			Three Functions	0:47
		Lecture Example 1		1:19
		Lecture Example 2		3:25
		Lecture Example 3		6:45
		Additional Example 4		2:02
		Additional Example 5		2:35
II. Limits
	Average and Instantaneous Rates of Change			20:59
		Intro		0:00
		Rates of Change		0:11
			Average Rate of Change	0:21
			Instantaneous Rate of Change	0:33
			Slope of the Secant Line	0:46
			Slope of the Tangent Line	1:00
		Lecture Example 1		1:14
		Lecture Example 2		6:36
		Lecture Example 3		11:30
		Additional Example 4		2:49
		Additional Example 5		3:40
	Limit Investigations			22:37
		Intro		0:00
		What is a Limit?		0:10
		Lecture Example 1		0:56
		Lecture Example 2		5:28
		Lecture Example 3		9:27
		Additional Example 4		4:42
		Additional Example 5		3:38
	Algebraic Evaluation of Limits			28:19
		Intro		0:00
		Evaluating Limits		0:09
		Lecture Example 1		1:06
		Lecture Example 2		5:16
		Lecture Example 3		8:15
		Lecture Example 4		12:58
		Additional Example 5		5:01
		Additional Example 6		5:35
	Formal Definition of a Limit			23:39
		Intro		0:00
		Formal Definition		0:13
			Template	0:55
			Epsilon and Delta	1:24
		Lecture Example 1		1:40
		Lecture Example 2		9:20
		Additional Example 3		2:52
		Additional Example 4		5:49
	Continuity and the Intermediate Value Theorem			19:09
		Intro		0:00
		Continuity		0:13
			Continuous	0:16
			Discontinuous	0:37
		Intermediate Value Theorem		0:52
			Example	1:22
		Lecture Example 1		2:58
		Lecture Example 2		9:02
		Additional Example 3		4:12
		Additional Example 4		2:23
III. Derivatives, part 1
	Limit Definition of the Derivative			22:52
		Intro		0:00
		Limit Definition of the Derivative		0:11
			Three Versions	0:13
		Lecture Example 1		1:02
		Lecture Example 2		4:33
		Lecture Example 3		6:49
		Lecture Example 4		10:11
		Additional Example 5		4:41
		Additional Example 6		5:18
	The Power Rule			26:01
		Intro		0:00
		Power Rule of Differentiation		0:14
			Power Rule with Constant	0:41
			Sum/Difference	1:15
		Lecture Example 1		1:59
		Lecture Example 2		6:48
		Lecture Example 3		11:22
		Additional Example 4		4:21
		Additional Example 5		3:51
	The Product Rule			14:54
		Intro
		Statement of the Product Rule		0:08
		Lecture Example 1		0:41
		Lecture Example 2		2:27
		Lecture Example 3		5:03
		Additional Example 4		4:11
		Additional Example 5		2:25
	The Quotient Rule			19:17
		Intro		0:00
		Statement of the Quotient Rule		0:07
			Carrying out the Differentiation	0:23
			Quotient Rule in Words	1:00
		Lecture Example 1		1:19
		Lecture Example 2		4:23
		Lecture Example 3		8:00
		Additional Example 4		5:46
		Additional Example 5		2:43
	Applications of Rates of Change			17:43
		Intro		0:00
		Rates of Change		0:11
		Lecture Example 1		0:44
		Lecture Example 2		5:16
		Lecture Example 3		7:38
		Additional Example 4		2:18
		Additional Example 5		3:54
	Trigonometric Derivatives			26:58
		Intro		0:00
		Six Basic Trigonometric Functions		0:11
			Patterns	0:47
		Lecture Example 1		1:18
		Lecture Example 2		7:38
		Lecture Example 3		12:15
		Lecture Example 4		14:25
		Additional Example 5		3:37
		Additional Example 6		5:27
	The Chain Rule			23:47
		Intro		0:00
		Statement of the Chain Rule		0:09
			Chain Rule for Three Functions	0:27
		Lecture Example 1		1:00
		Lecture Example 2		4:34
		Lecture Example 3		7:23
		Additional Example 4		5:05
		Additional Example 5		5:38
	Inverse Trigonometric Functions			27:05
		Intro		0:00
		Six Basic Inverse Trigonometric Functions		0:10
		Lecture Example 1		1:11
		Lecture Example 2		8:53
		Lecture Example 3		12:37
		Additional Example 4		7:05
		Additional Example 5		4:02
	Equation of a Tangent Line			15:52
		Intro		0:00
		Point Slope Form		0:10
		Lecture Example 1		0:47
		Lecture Example 2		3:15
		Lecture Example 3		6:10
		Additional Example 4		3:27
		Additional Example 5		3:01
IV. Derivatives, part 2
	Implicit Differentiation			30:05
		Intro		0:00
		Purpose		0:09
			Implicit Function	0:20
		Lecture Example 1		0:32
		Lecture Example 2		7:14
		Lecture Example 3		11:22
		Lecture Example 4		16:43
		Additional Example 5		3:55
		Additional Example 6		5:04
	Higher Derivatives			13:16
		Intro		0:00
		Notation		0:08
			First Type	0:19
			Second Type	0:54
		Lecture Example 1		1:41
		Lecture Example 2		3:15
		Lecture Example 3		4:57
		Additional Example 4		4:04
		Additional Example 5		1:24
	Logarithmic and Exponential Function Derivatives			17:42
		Intro		0:00
		Essential Equations		0:12
		Lecture Example 1		1:34
		Lecture Example 2		2:48
		Lecture Example 3		5:54
		Additional Example 4		4:18
		Additional Example 5		4:51
	Hyperbolic Trigonometric Function Derivatives			14:30
		Intro		0:00
		Essential Equations		0:15
			Six Basic Hyperbolic Trigc Functions	0:32
			Six Basic Inverse Hyperbolic Trig Functions	1:21
		Lecture Example 1		1:48
		Lecture Example 2		3:45
		Lecture Example 3		7:09
		Additional Example 4		2:12
		Additional Example 5		3:03
	Related Rates			29:05
		Intro		0:00
		What Are Related Rates?		0:08
		Lecture Example 1		0:35
		Lecture Example 2		5:25
		Lecture Example 3		11:54
		Additional Example 4		4:04
		Additional Example 5		6:52
	Linear Approximation			23:52
		Intro		0:00
		Essential Equations		0:09
			Linear Approximation (Tangent Line)	0:18
			Example: Graph	1:18
			Differential (df)	2:06
			Delta F	5:10
		Lecture Example 1		6:38
		Lecture Example 2		11:53
		Lecture Example 3		15:54
		Additional Example 4		2:56
		Additional Example 5		2:38
V. Application of Derivatives
	Absolute Minima and Maxima			18:57
		Intro		0:00
		Minimums and Maximums		0:09
			Absolute Minima and Maxima (Extrema)	0:53
			Critical Points	1:25
		Lecture Example 1		2:58
		Lecture Example 2		6:57
		Lecture Example 3		10:02
		Additional Example 4		3:19
		Additional Example 5		2:34
	Mean Value Theorem and Rolle's Theorem			20:00
		Intro		0:00
		Theorems		0:09
			Mean Value Theorem	0:13
			Graphical Explanation	0:36
			Rolle's Theorem	2:06
			Graphical Explanation	2:28
		Lecture Example 1		3:36
		Lecture Example 2		6:33
		Lecture Example 3		9:32
		Additional Example 4		2:27
		Additional Example 5		2:52
	First Derivative Test, Second Derivative Test			27:11
		Intro		0:00
		Local Minimum and Local Maximum		0:14
			Example	1:01
		First and Second Derivative Test		1:26
			First Derivative Test	1:36
			Example	2:00
			Second Derivative Test (Concavity)	2:58
			Example: Concave Down	3:15
			Example: Concave Up	3:54
			Inconclusive	4:19
		Lecture Example 1		5:23
		Lecture Example 2		12:03
		Lecture Example 3		15:54
		Additional Example 4		4:34
		Additional Example 5		2:52
	L'Hopital's Rule			23:09
		Intro		0:00
		Using L'Hopital's Rule		0:09
			Informal Definition	0:34
		Lecture Example 1		1:27
		Lecture Example 2		4:00
		Lecture Example 3		5:40
		Lecture Example 4		9:38
		Additional Example 5		4:50
		Additional Example 6		6:32
	Curve Sketching			40:16
		Intro		0:00
		Collecting Information		0:15
			Domain and Range	0:17
			Intercepts	0:21
			Symmetry Properties (Even/Odd/Periodic)	0:33
			Asymptotes (Vertical/Horizontal/Slant)	0:45
			Critical Points	1:15
			Increasing/Decreasing Intervals	1:24
			Inflection Points	1:38
			Concave Up/Down	1:52
			Maxima/Minima	2:03
		Lecture Example 1		2:58
		Lecture Example 2		10:52
		Lecture Example 3		17:55
		Additional Example 4		12:57
		Additional Example 5		4:38
	Applied Optimization			25:37
		Intro		0:00
		Real World Problems		0:08
			Sketch	0:11
			Interval	0:20
			Rewrite in One Variable	0:26
			Maximum or Minimum	0:34
			Critical Points	0:42
			Optimal Result	0:52
		Lecture Example 1		1:05
		Lecture Example 2		6:12
		Lecture Example 3		13:31
		Additional Example 4		2:37
		Additional Example 5		4:03
	Newton's Method			25:13
		Intro		0:00
		Approximating Using Newton's Method		0:10
			Good Guesses for Convergence	0:32
		Lecture Example 1		0:49
		Lecture Example 2		4:21
		Lecture Example 3		7:59
		Additional Example 4		5:13
		Additional Example 5		7:06
VI. Integrals
	Approximating Areas and Distances			36:50
		Intro		0:00
		Three Approximations		0:12
			Right Endpoint, Left Endpoint, Midpoint	0:22
			Formulas	1:05
			Velocity and Distance	1:35
		Lecture Example 1		2:28
		Lecture Example 2		12:10
		Lecture Example 3		19:43
		Additional Example 4		5:43
		Additional Example 5		4:08
	Riemann Sums, Definite Integrals, Fundamental Theorem of Calculus			22:02
		Intro		0:00
		Important Equations		0:22
			Riemann Sum	0:28
			Integral	1:58
			Integrand	2:35
			Limits of Integration (Upper Limit, Lower Limit)	2:43
			Other Equations	3:05
			Fundamental Theorem of Calculus	4:00
		Lecture Example 1		5:04
		Lecture Example 2		10:43
		Lecture Example 3		13:52
		Additional Example 4		2:59
		Additional Example 5		3:20
	Substitution Method for Integration			23:19
		Intro		0:00
			U-Substitution	0:13
		Important Equations		0:30
			Purpose	0:36
		Lecture Example 1		1:30
		Lecture Example 2		6:17
		Lecture Example 3		9:00
		Lecture Example 4		11:24
		Additional Example 5		2:10
		Additional Example 6		3:48
VII. Application of Integrals, part 1
	Area Between Curves			19:59
		Intro		0:00
		Area Between Two Curves		0:12
			Graphic Description	0:34
		Lecture Example 1		1:44
		Lecture Example 2		5:39
		Lecture Example 3		8:45
		Additional Example 4		3:37
		Additional Example 5		3:01
	Volume by Method of Disks and Washers			24:22
		Intro		0:00
		Important Equations		0:16
			Equation 1: Rotation about x-axis (disks)	0:27
			Equation 2: Two curves about x-axis (washers)	3:38
			Equation 3: Rotation about y-axis	5:31
		Lecture Example 1		6:05
		Lecture Example 2		8:28
		Lecture Example 3		11:55
		Additional Example 4		4:12
		Additional Example 5		2:46
	Volume by Method of Cylindrical Shells			30:29
		Intro		0:00
		Important Equations		0:50
			Equation 1: Rotation about y-axis	1:04
			Equation 2: Rotation about y-axis (2 curves)	7:34
			Equation 3: Rotation about x-axis	8:15
		Lecture Example 1		8:57
		Lecture Example 2		14:26
		Lecture Example 3		18:15
		Additional Example 4		4:45
		Additional Example 5		3:45
	Average Value of a Function			16:31
		Intro		0:00
		Important Equations		0:11
			Origin of Formula	0:34
		Lecture Example 1		2:51
		Lecture Example 2		5:30
		Lecture Example 3		8:13
		Additional Example 4		2:40
		Additional Example 5		3:23
VIII. Extra
	Graphs of f, f', f''			23:58
		Intro		0:00
		Slope Function of f(x)		0:41
			Slope is Zero	0:53
			Slope is Positive	1:03
			Slope is Negative	1:13
		Slope Function of f'(x)		1:31
			Slope is Zero	1:42
			Slope is Positive	1:48
			Slope is Negative	1:54
		Lecture Example 1		2:23
		Lecture Example 2		8:06
		Lecture Example 3		12:36
		Additional Example 4		3:11
		Additional Example 5		3:31
	Slope Fields for Differential Equations			18:32
		Intro		0:00
		Things to Remember		0:13
			Graphic Description	0:42
		Lecture Example 1		1:44
		Lecture Example 2		6:59
		Lecture Example 3		9:46
		Additional Example 4		3:09
		Additional Example 5		2:01
	Separable Differential Equations			17:04
		Intro		0:00
		Differential Equations		0:10
			Focus on Exponential Growth/Decay	0:27
			Separating Variables	0:47
		Lecture Example 1		1:35
		Lecture Example 2		6:41
		Lecture Example 3		9:36
		Additional Example 4		2:56
		Additional Example 5		2:10

Educator

the best free way to manage your classroom

Free Class Website!

Free Unlimited Hosting!

Free Educator.com Domain!

L'Hopital's Rule

Share this knowledge with your friends!

Start Learning Now

Features Overview

L'Hopital's Rule

L'Hopital's Rule

Mathematics: College Calculus: Level I

Related Books

Related Books

	Calculus by Larson, 9th Edition Authors: Ron Larson, Bruce H. Edwards ISBN: 547167024 Publisher: Brooks Cole Year: 2009 The book is filled with examples and detailed explanations. Capstone exercises are also included for each section and synthesize the main concepts into a single example.
	Calculus by Larson, 9th Edition, Solutions Manual, Volume 1 Author: Ron Larson ISBN: 547213093 Publisher: Brooks Cole Year: 2008 This solutions manual includes worked out solutions to every odd-numbered exercise in Calculus of a Single Variable, 9th edition.
	Calculus by Larson, 9th Edition, Solutions Manual, Volume 2 Authors: Ron Larson, Bruce H. Edwards ISBN: 547213107 Publisher: Brooks Cole Year: 2009 This solutions manual includes worked out solutions to every odd-numbered exercise in Multivariable Calculus, 9th edition.