Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of College Calculus: Level I
For more information, please see full course syllabus of College Calculus: Level I
College Calculus: Level I Limit Definition of the Derivative
Lecture Description
In this lesson we are going to talk about continuity and the intermediate value theorem. In fact, intermediate value theorem represents the application of the continuity. First, we will give definitions of continuity and the intermediate value theorem. Simple illustration will be given just to clarify the meaning of intermediate value theorem. Later on, we will do some examples where we will be looking for places at which the function is not continuous, such are: removable discontinuities, jump discontinuities, and infinite discontinuities. We will also be looking for places where the function is not even defined because these are discontinuities as well.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine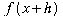 - it is a function composition!
- it is a function composition! 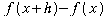 ; realize we are subtracting off the entire quantity given by
; realize we are subtracting off the entire quantity given by 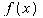 .
. 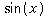 and
and 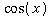 is famous and involves a couple famous limits.
is famous and involves a couple famous limits. 





0 answers
Post by Nadia Ariqat on April 8, 2014
very cool! you do a great job…i've never taken calculus before and just happened to be browsing..kind of want to take the actual course now!
0 answers
Post by Jose Gonzalez-Gigato on April 9, 2013
Great teaching! Thanks!
2 answers
Last reply by: Erika O
Wed Mar 13, 2013 4:10 PM
Post by Erika O on March 5, 2013
All of the calculus books and course material I have uses Δx instead of h as a variable. Is there a reason that it is different here?
0 answers
Post by Hanna Flanagan on September 12, 2012
what about finding the derivitave of 3x^2+1 at x=-1 using this formula?
3 answers
Last reply by: Angela Patrick
Mon Nov 25, 2013 12:40 PM
Post by Moniyka Sachar on September 26, 2010
It would be great if educator.com added an additional part to this sequence, about graphing derivatives and relating them to the original graph, because those can be tricky. Otherwise, thanks!