Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of College Calculus: Level I
For more information, please see full course syllabus of College Calculus: Level I
College Calculus: Level I The Quotient Rule
Lecture Description
In this lesson we will take a look at the Quotient Rule. The Quotient Rule is a method of finding the derivative of a function that is the quotient of two other functions for which derivatives exist. The Quotient Rule says that the derivative of a quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator. Through several examples we will see how to use The Quotient Rule when calculating the derivative of functions.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine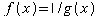 can be re-written as
can be re-written as 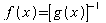 if you prefer the Chain Rule to the Quotient Rule.
if you prefer the Chain Rule to the Quotient Rule. 





1 answer
Mon Nov 12, 2018 6:56 PM
Post by Samatar Farah on November 2, 2018
The audio file for examples 4 and 5 don't exist.
0 answers
Post by Mohamed Al Mohannadi on September 11, 2016
We can further simply "Lecture Example 1."
We can write -16 / (6x-5)^2 as - [ 4 / 6x - 5 ] ^ 2
Am I right?
0 answers
Post by Ashley Simon on May 5, 2015
at 3:38, why is 6 negative??
0 answers
Post by Chateau Siqueira on September 3, 2013
Where Can I find a Lecture about the Difference quotient? Thanks!
1 answer
Last reply by: Martina Alvarez
Tue Dec 6, 2011 1:20 PM
Post by naman ahmad on October 24, 2011
on the last additional problem, last step we had:(e^x+7)-(Xe^x)/(e^x+7)^2. we could have cancelled out the e^x+7 and remained with -Xe^x/e^x+7.
1 answer
Last reply by: Stefán Berg Jansson
Fri Nov 25, 2011 7:10 PM
Post by Xiaosong Gao on January 17, 2011
example 3 can be further simplified to: 3^(1/2)x/1+x^3
1 answer
Last reply by: Larry Davis
Wed Sep 15, 2010 10:25 AM
Post by Larry Davis on September 15, 2010
on ex 2 you used the wrongterms in the numerator. it should have been ex d/dx[X8]-
X8 d/dx[ex]/[x8]2 gives you =ex(8-x)/X9