Click video to play

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Multivariable Calculus
For more information, please see full course syllabus of Multivariable Calculus
Multivariable Calculus More on Vectors & Norms
Lecture Description
Last lesson we introduced the scalar product, or dot product. We also talked a little bit about norms. In this lesson, we are going to talk more about norms and vectors. The first part of the lesson, is going to be basic properties - things that are pretty intuitively clear, but we want to formalize them, things that we are going to be talking about at any given moment. We are going to be talking about open discs, open balls, and we want to make sure that we understand what these are, that we have been exposed to them so that we can proceed with our discussion of multivariable Calculus.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine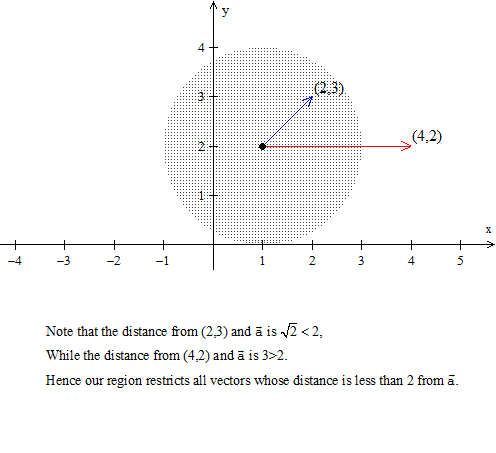






1 answer
Mon Dec 21, 2015 7:42 PM
Post by Jamal Tischler on December 21, 2015
We could say at the projection of a vector just, ||a|| cos(tetha)* b/||b||. Where ||a|| cos (tetha) is the legth of the projection( in the right triangle, I applied cos) and b/||b|| is the init vector along b.
1 answer
Wed Jan 28, 2015 12:38 PM
Post by Jacob Kalbfleisch on January 25, 2015
Prof. Hovasapian is hands down the best lecturer on Educator. So clear and succinct, and offers fantastic advice very bluntly. I've so much respect for this man!
4 answers
Fri Jun 20, 2014 4:50 PM
Post by abc def on June 11, 2014
Good morning Professor Hovasapian,
I was playing around with some Angle-Difference Identities to wrap my mind around the dot product in 2-3D. I observed that A*B = ||A||||B||cos(@) can be proven by using the Angle-Difference Identity in respect of cos(@),
A*B=||A||||B||cos(@a - @b) = ||A||||B||[cos(@a)cos(@b)+sin(@a)sin(@b)] = [||A||cos(@a)||B||cos(@b)+||A||sin(@a)||B||sin(@b)] = (Ax)(Bx)+(Ay)(By) QED.
Is there a operation that _____=||A||||B||sin(@) would work?
1 answer
Wed Oct 2, 2013 2:50 PM
Post by Said Sabir on October 2, 2013
how to calculate the angel if I know already the Cos of that angel ?