Starting up...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Multivariable Calculus
For more information, please see full course syllabus of Multivariable Calculus
Multivariable Calculus Triple Integrals
Lecture Description
In this lesson we are going to start talking about triple integrals and the nice thing about is that there is actually nothing new to learn - you just need to integrate three times and that's it. We will first do a quick couple of words and then we will just get right to the examples, because that is what is important. Remember that for single integrals, we integrate it over a length. For a double integral, we integrate it over an area. Accordingly, for triple integrals, we are now integrating over a region in 3-space, which is a volume.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine
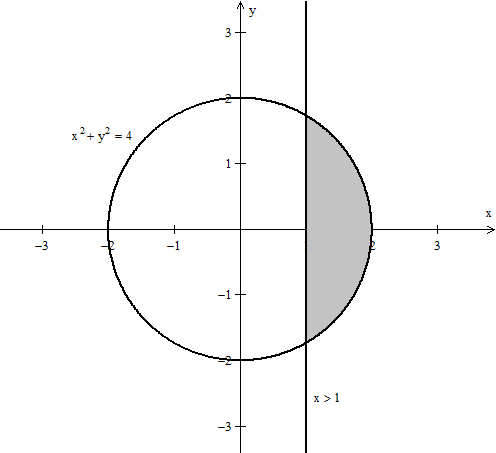
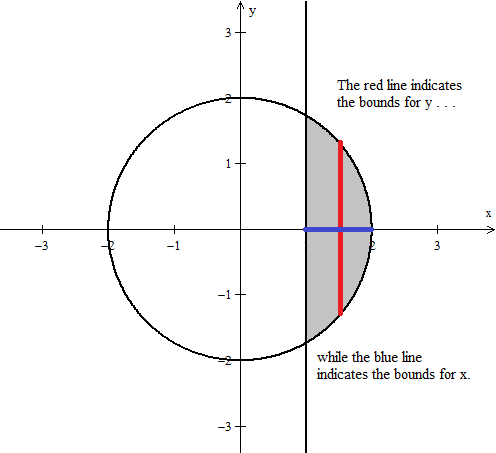
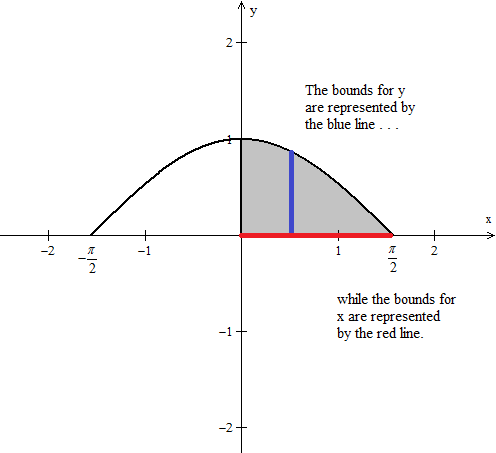





1 answer
Thu May 1, 2014 9:59 PM
Post by Andi Bislimi on May 1, 2014
Why can't I forward the video? I always have to wait until it loads to the point I am interested in..
1 answer
Thu Dec 26, 2013 3:05 PM
Post by Atreya Mohile on December 26, 2013
Hi prof. Hovasapian,
In many books and maths questions, I saw that the non-integrable functions, can be integrated till some limit (geometrically), so my doubt is that how to integrate such functions by traditional method, especially in 3D integrals?
1 answer
Sat Aug 3, 2013 10:37 PM
Post by Waleed Junaidy Waleed Junaidy on August 3, 2013
why are we integrating 1 in the first example?
2 answers
Last reply by: Gregory Gutierrez
Thu Nov 3, 2016 3:01 AM
Post by Josh Winfield on May 19, 2013
Hey Raffi , assuming your error in Example 3 where pi is the radius of the sphere is accounted for, why have you ignored the area bounded by y=sinx and y=2sinx for values of x <0 and >-pi as you did not state bounded by the xy plane in the probelm, shouldn't that are be taken into consideration and if it was is the integral =0
1 answer
Mon Sep 3, 2012 10:54 PM
Post by Mohammed Alhumaidi on September 3, 2012
In the last example of sin and 2sin...
Why you did not include the region bounded by the x-y plane from Pi to 2Pi ? Is that because the radius of the sphere is 2 therefore it is less than Pi ?
And if supposing that the radius of the sphere is bigger than Pi (e.g. 9) would it be correct to take the limits of integration from 0 to 2Pi ?