Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Trigonometry
For more information, please see full course syllabus of Trigonometry
Trigonometry Computations of Inverse Trigonometric Functions
Lecture Description
This lecture covers the computations of inverse trigonometric functions. You'll learn the values of the inverse trig functions for some special angles, using the unit circle. It is important to know where these inverse functions are defined and where their answers lie. The domain of the sine is the range of the arcsine, while the range of the sine is the domain of the arcsine. This applies for the other two as well. You'll also learn which of these functions is even, which is odd and which is neither. This could be determined from both the graph and the equation of the function.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine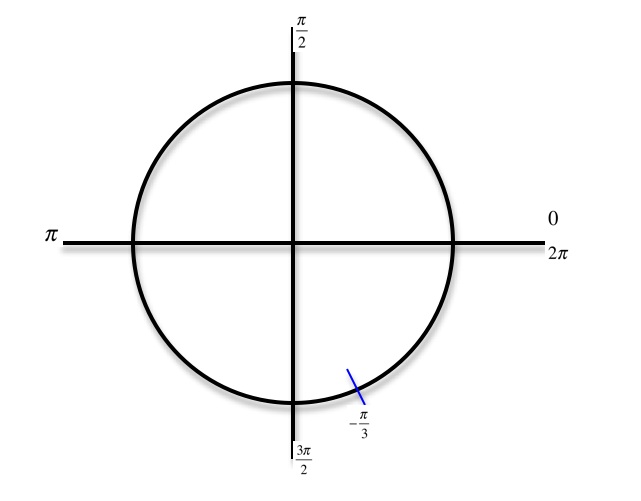



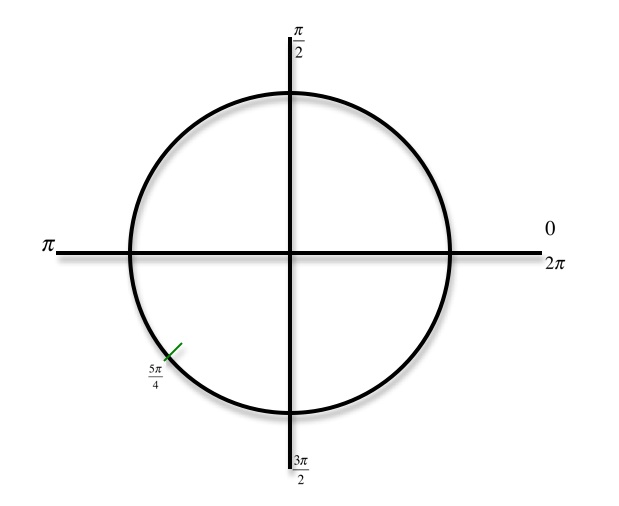
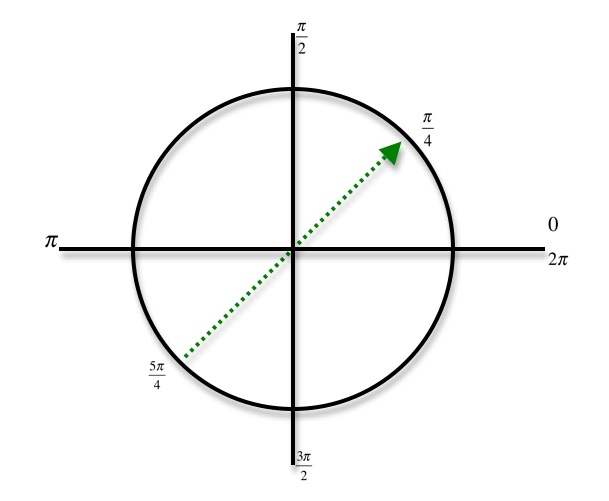
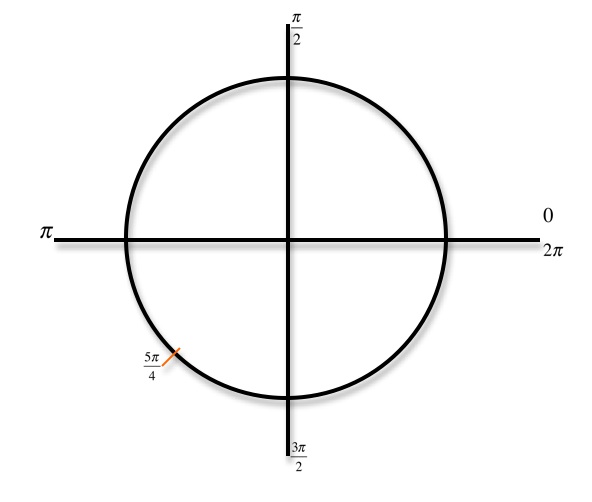


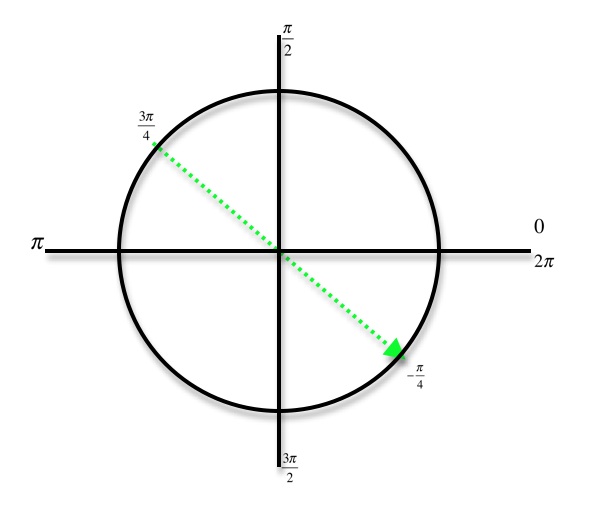
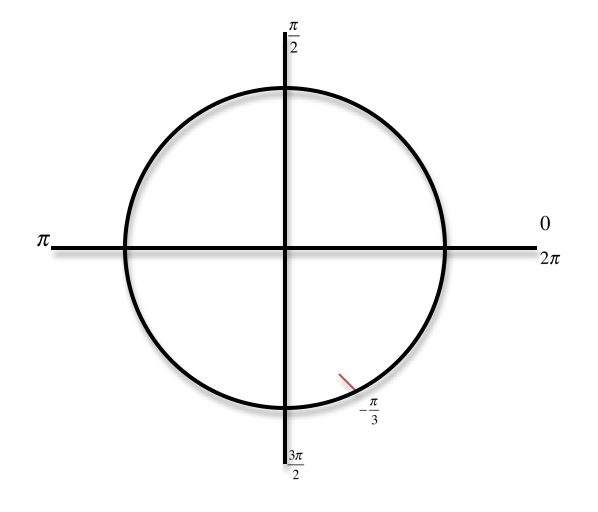
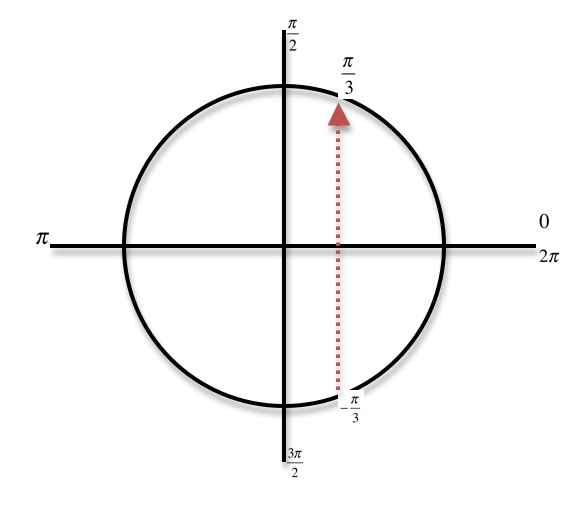




1 answer
Wed Jun 24, 2020 11:02 AM
Post by Victoria Su on June 23, 2020
Hello,
I am not quite sure how you got the answers for the arcsines, arccosines, and arctangents for the extra example 2. I understand the sine, cosine, and tangent values on the unit circle, I just don't know how you got the arcsine, arctangent, and arccosine.
1 answer
Fri Apr 3, 2020 10:02 AM
Post by Cheung Chun Hei on April 1, 2020
Hi professor Murray, I am not really familiar with Trigonometry. I can catch up the previous lesson but I am not understanding about example one in this lecture. How do you figure out those arcsine values?
1 answer
Mon Aug 4, 2014 8:19 PM
Post by adnan akram on July 17, 2014
In example 1 how 30 degrees is pi/3 and 60 degrees is also pi/3 why? according what I know 30 degrees is pi/6 and 60 is pi/3
Thank you!!
2 answers
Mon Oct 21, 2013 7:32 PM
Post by Robert Mills on October 15, 2013
Between example 1 & 3, I'm confused as to why the arcsinx mirror eachother, meaning why is -1 arcsinx = -π/2, but 1 arcsinx = π/2? On the unit circle, the angle for 1 arcsinx reads 3π/2. I'm just missing some knowledge here, thank you!
1 answer
Wed Aug 14, 2013 12:25 PM
Post by Kiyoshi Smith on August 8, 2013
In Example 3 you give arcsin(-(2)^(1/2)/2) as 3pi/2 when it should be 3pi/4. I thought I should point this out.
4 answers
Thu Jul 18, 2013 8:26 AM
Post by Mark Mercready on December 22, 2011
In Example 1 you give arcsin(-1/2) as -pi/3 when it should be pi/6. And for arcsin(1/2) you give pi/3 when it is pi/6. Please correct this.
1 answer
Wed Apr 3, 2013 11:34 AM
Post by Cain Blaha on November 28, 2011
how would you solve if the angle you were trying to find was not part of a special triangle?
Ex. sin(arccos(3/4))
1 answer
Wed Apr 3, 2013 11:27 AM
Post by Tanielle Spencer on October 28, 2011
my unit circle is not matching his although i follow his concept.
7 answers
Thu Mar 27, 2014 4:51 PM
Post by Hero Miles on May 15, 2011
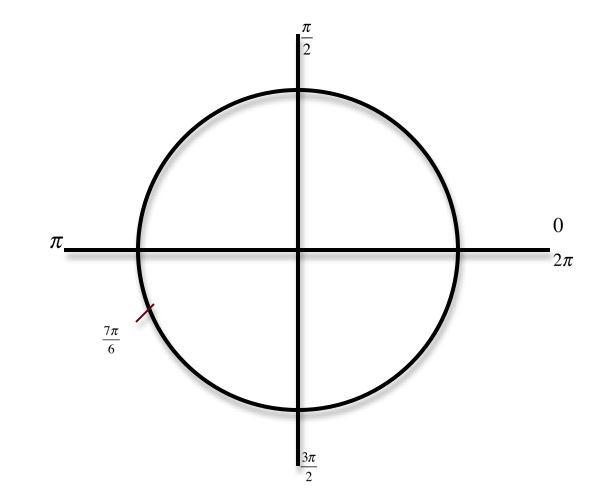
Timothy, 7pi/6 is on the unit circle. In order to solve your problem you have to evaluate sin 7pi/6 first. Then evaluate inverse cosine of that:
arcos(sin 7pi/6)= arcos(-1/2) = 2pi/3
Piece of cake.
1 answer
Wed Apr 3, 2013 11:24 AM
Post by Timothy Harris on February 18, 2011
this video is very helpful except, what about values that are no on the unit circle or the problems aren't exactly like what is shown
ex: arccos(sin 7pi/6)