Starting up...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Trigonometry
For more information, please see full course syllabus of Trigonometry
Trigonometry Tangent and Cotangent Functions
Lecture Description
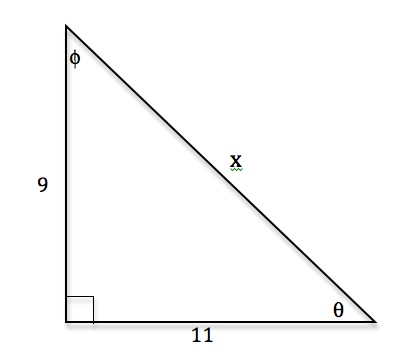
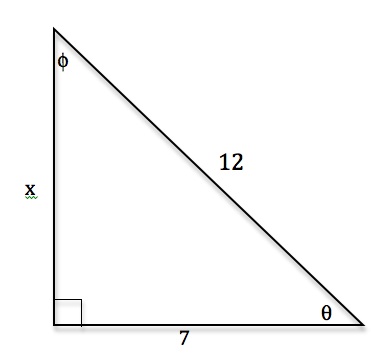
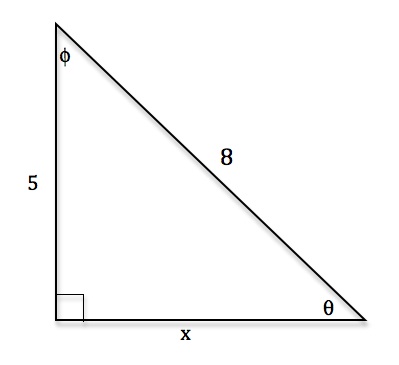
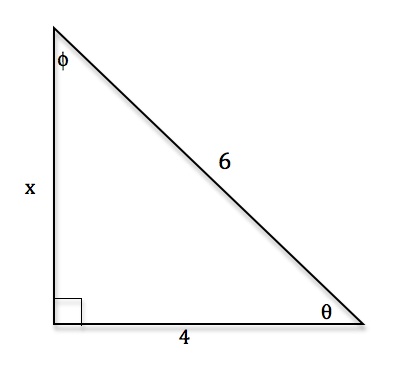
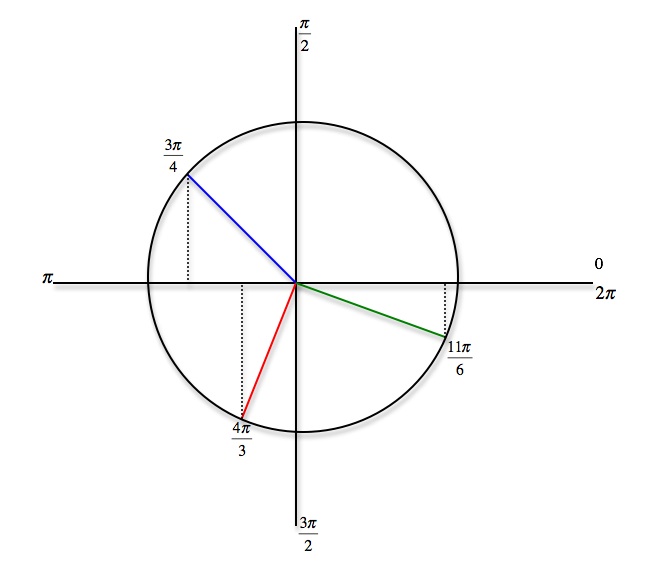
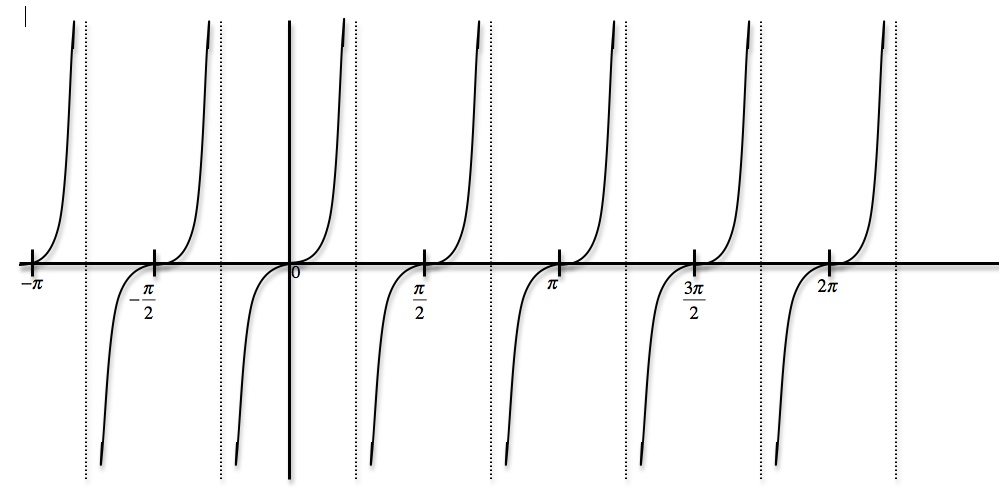
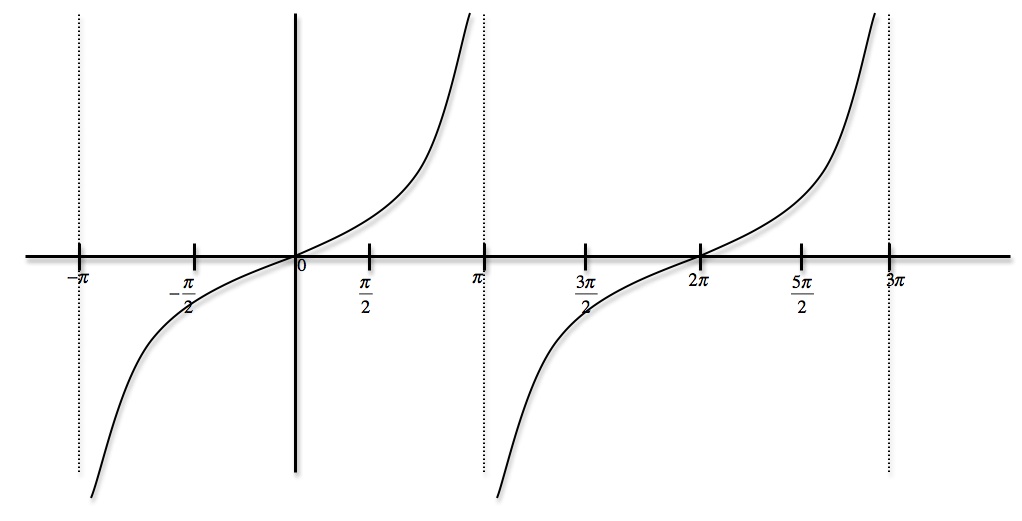
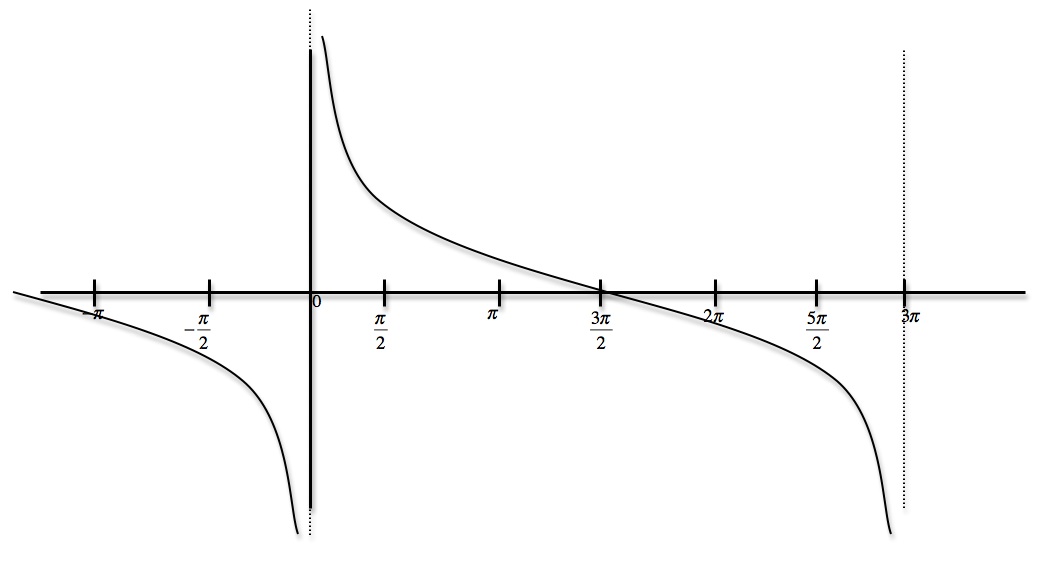
Tangent is defined as a quotient of sine and cosine so when cosine is zero, the tangent is not defined. On the other hand, cotangent is defined as a quotient of cosine and sine so it's not defined when sine is zero. You can also apply the Sohcahtoa rule here. This, of course, applies only to a right triangle. If you remember the common values of sine and cosine you can always work out the common values of tangent and cotangent. However, a right angle is a tricky one. This lecture also covers the uses of tangent and teaches you the sign of tangent in different quadrants.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine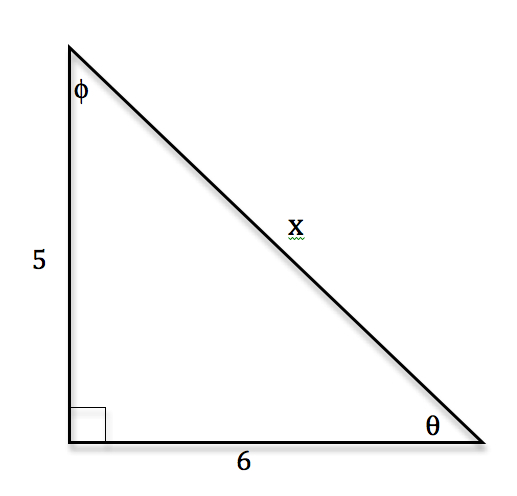





1 answer
Tue Aug 5, 2014 3:47 PM
Post by Jason Wilson on July 23, 2014
In example 4, TAN = SIN/COS, is that 1/2 over negative sqrt3 / 2 which evaluates to "- sqrt3 over 4" ?? you said one over sqrt3 that evaluates to negative sqrt3/3 please help thx
1 answer
Fri Jul 5, 2013 9:52 AM
Post by Matthew Chantry on June 30, 2013
The practice question for this is a secant/cosecant question, which hasn't been covered yet. This may be an error.
Thanks.
1 answer
Fri Jun 21, 2013 6:16 PM
Post by HAFSA Ahmad on June 12, 2013
I still don't understand how to figure out the angle in radians like in this example 5pi/6 , 5pi/4 etc.
2 answers
Tue Jan 1, 2013 11:34 AM
Post by Jorge Sardinas on December 31, 2012
how did you turn sin[-x]/cos[-x into -sin x/cos x ; ->
1 answer
Tue Jan 1, 2013 11:25 AM
Post by Ahmed Shiran on April 18, 2011
This is interesting lecture ! thanks :-)