Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Trigonometry
For more information, please see full course syllabus of Trigonometry
Trigonometry in Right Angles
Lecture Description
The most common use of trigonometry is in right triangles. There are formulas for the sine, cosine and tangent of the acute angle in a right triangle. The shortcut to remember these formulas is known as SOHCAHTOA, which is explained in detail in this lecture. If you're having trouble remembering the word SOHCAHTOA, there's a mnemonic that'll help you remember it more easily. You'll learn how to solve the right triangle using trigonometry. It is important to know that SOHCAHTOA only works in right triangles. For other triangles there are some other rules that can be used, which will be covered in the next lecture.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine
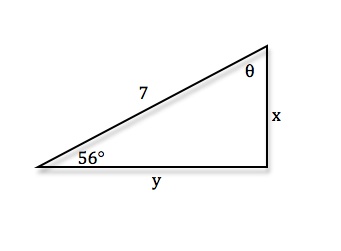
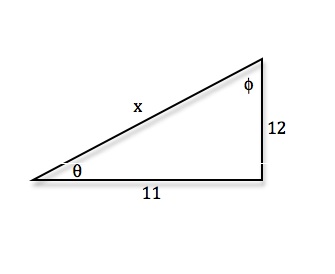
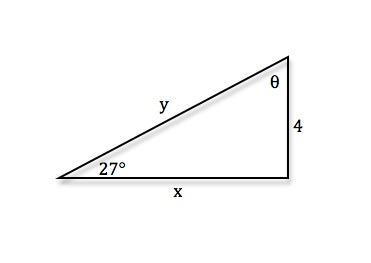
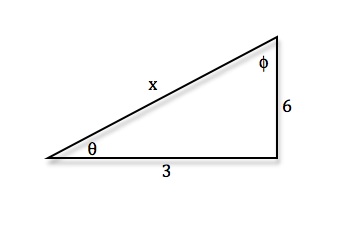




1 answer
Sun Oct 4, 2020 12:02 PM
Post by Hong Yang on October 3, 2020
thanks sir, this course helped me out a lot
1 answer
Mon Jul 20, 2020 11:29 AM
Post by Erika Wu on July 18, 2020
on number three example trying to figure out "fee" you want need to use the soh part of sohcahtoa since you know 180 - 90- 62.8 is 21.8
1 answer
Wed Oct 14, 2015 4:44 PM
Post by Vance Bower on October 14, 2015
Can you use sin, cosin, or tangent in any order for angle theta or c to get the angle measurements? In other words, you used the tan of theta and the sin of c in the third example. Could I have used the tangent of theta and the cosign or tangent of c, instead of the sin of c?
2 answers
Tue Aug 5, 2014 11:50 AM
Post by Joshua Jacob on July 19, 2014
Sorry if this is a little unrelated but is it possible to do arcsin, arccos, and arctan on a graphing calculator? Is it the same thing as sin^-1...etc.
Thank you for making these amazing lectures!
1 answer
Thu Jul 18, 2013 8:25 AM
Post by Manfred Berger on July 7, 2013
Unless I'm missing anything crucial here, the fact that SOCAHTOA only works for right triangles stems directly from the basic definition of the the unit circle, which is essentially the pythagorian theorem.
1 answer
Mon May 6, 2013 8:54 PM
Post by Emily Engle on May 5, 2013
How would you solve for the inverse ratios without a calculator?