Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Trigonometry
For more information, please see full course syllabus of Trigonometry
Trigonometry Finding the Area of a Triangle
Lecture Description
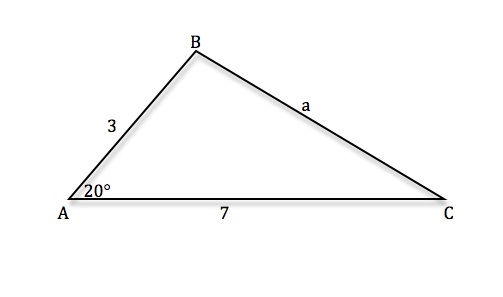
There are different methods to find the area of triangles and choosing which method to use depends on the type of initial data you have. The formula for the area of a triangle is still one-half of base times height, but these rules will help you get all the data you need for that formula. In different examples you'll see how to find the area of a triangle if you are given two sides and one angle, or the area of a triangle if you know all the three sides (this could be done in more than one way). This lecture requires the knowledge of previous lectures: the SOHCAHTOA, the Law of Cosines, and the Heron's Formula.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine




1 answer
Wed Aug 17, 2016 3:19 PM
Post by Julian Xiao on August 17, 2016
Doesn't the Heron's formula have a typo at around 3:00?
1 answer
Wed Aug 14, 2013 12:05 PM
Post by Ikze Cho on August 7, 2013
does heron's formula work for all triangles? Thanks
1 answer
Thu May 30, 2013 4:09 PM
Post by Mark Mccraney on January 19, 2010
III, lecture 4, 13:55, the supplemental angle is figured as 180-121.6=59.4 This is incorrect; the answer is 58.4 and throws off the Area by almost 3/10. Answer should come out to approx. 26.8 vs 27.1 given.
1 answer
Thu May 30, 2013 4:06 PM
Post by Mark Mccraney on January 19, 2010
My highschooler informed me today how they learned SOHCAHTOA since TOA could get reversed: taking away oats or taking oats away. The high school version is Some Old Hippie Caught Another Hippie Tripping On Acid!!! Can't get that one twisted!!!