Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Algebra 2
For more information, please see full course syllabus of Algebra 2
Algebra 2 Exponential Functions
Lecture Description
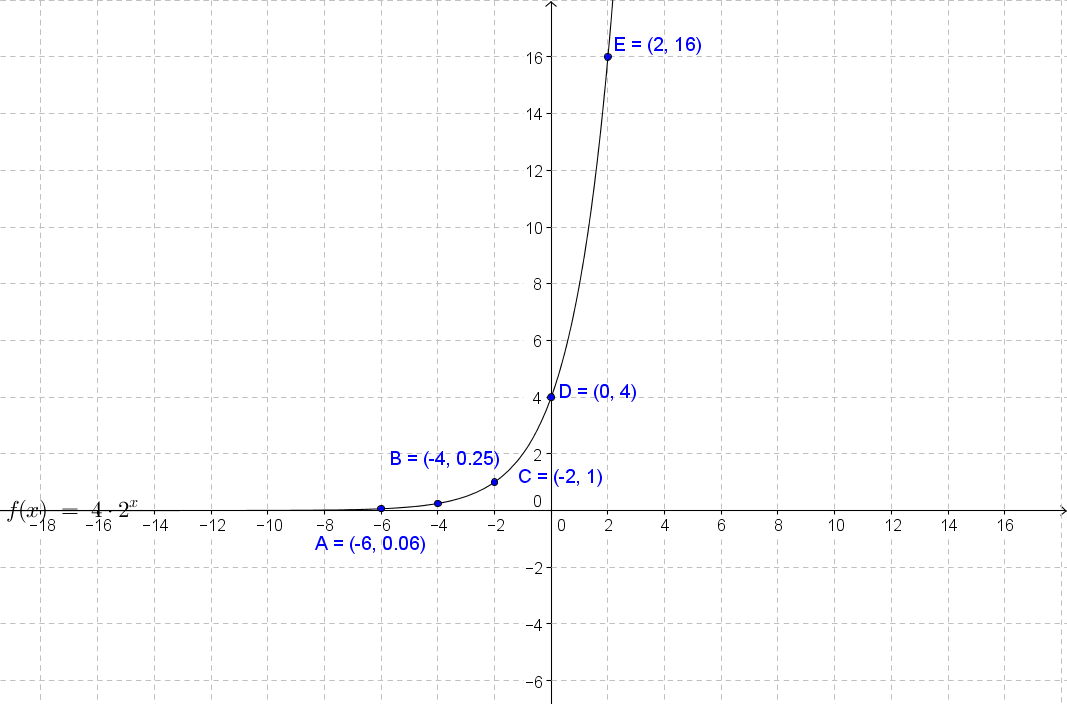
Exponential functions are the functions that have x in the exponent. The base of the exponential function is a positive number, and whether it's greater than 1 or not defines how the graph will look like. If the base is greater than 1, the function is exponential growth. If it is between 0 and 1, it is exponential decay. To graph the exponential function, we can use the table. To solve exponential equations with the same base, equate the exponents. To solve exponential inequalities with the same base, apply the same inequality to the exponents.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture









































 Carleen Eaton
Carleen Eaton Grant Fraser
Grant Fraser
 Answer Engine
Answer Engine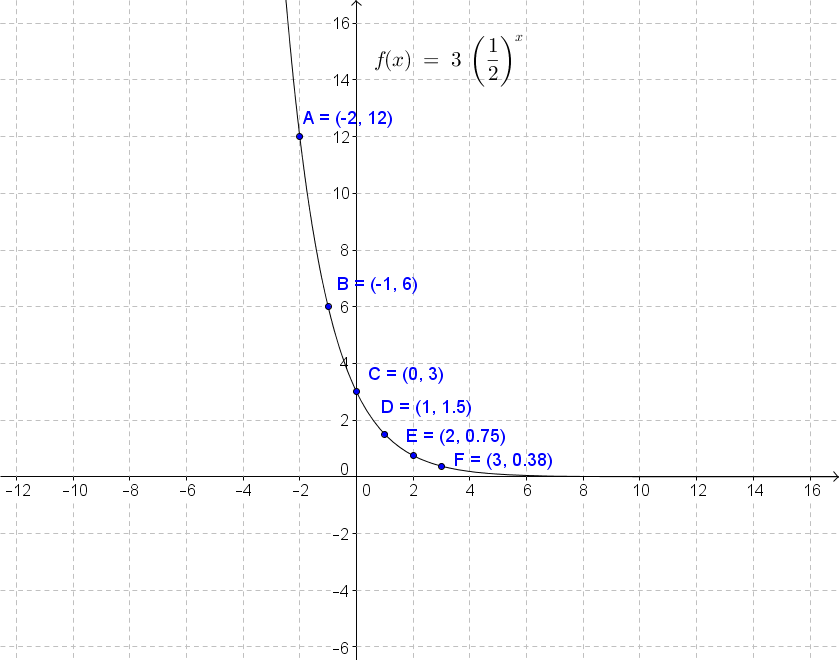




2 answers
Last reply by: Jerry Jin
Wed Jul 24, 2019 11:06 AM
Post by Matthew Johnston on August 8, 2016
In example 3 shouldn't 8/38=4/19 instead of 2/19?
0 answers
Post by Krishna Vempati on April 6, 2015
I watched this lecture and I tried solving a problem in math class but I had trouble here is the problem.....
Your parents offer to pay you exponentially to study for your Algebra test. They say that if you study for one hour you'll get $6, two hours gets you a total $7, three hours $9, four hours $13, etc. What equation are they using to come up with those values?
Could you please help me solve this?
1 answer
Sun Mar 15, 2015 11:20 PM
Post by Daija Jenkins on March 9, 2015
Directions: Write an exponential function for the graph that passes through the given points.
How do I solve: (0,-5)and (-3, -135)
1 answer
Sat Sep 14, 2013 2:58 PM
Post by Tami Cummins on August 27, 2013
Isn't negative 3 raised to a negative 2 power still a positive 1/9. When you square the negative 3 doesn't it become positive?
1 answer
Tue Jul 3, 2012 7:24 PM
Post by Laura Gilchrist on June 27, 2012
If there is no variable in the exponent, will it just be a power function instead? Does it have to have variable for it to be exponential? Thanks!!
1 answer
Mon Apr 16, 2012 10:18 PM
Post by Ed Grommet on April 13, 2012
FOr some reason it will not play. Question is IF i have a expo equations of y=-5^x same as y=(-1)(5^x) ? Also is it decay or growth since it is not above the x axis?
1 answer
Mon Mar 19, 2012 3:51 PM
Post by Ding Ye on March 19, 2012
This is a really nice video. Thanks a lot!
1 answer
Thu Jan 26, 2012 7:53 PM
Post by Jose Gonzalez-Gigato on January 24, 2012
In the slide labeled 'Properties', at about 12:50, you mention f(x) is 'one-to'one' and give the reason that it passes the vertical line test. For a function to be 'one-to-one' it must pass the horizontal line test.
1 answer
Wed Jan 11, 2012 12:38 AM
Post by Arlene Francis on January 9, 2012
Are there extra examples of problems.
1 answer
Wed Dec 28, 2011 9:10 PM
Post by Jonathan Taylor on December 27, 2011
Dr carleen must the base be the same in all exponential equation are is this only when your working with certain exponential fuction
0 answers
Post by Guillermo Marin on August 8, 2010
Dr. Eaton is really OUTSTANDING!
0 answers
Post by Dr Carleen Eaton on May 18, 2010
Correction to Example III: The solution, x = 8/38 reduces to 4/19, not 2/19