Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Algebra 2
For more information, please see full course syllabus of Algebra 2
Algebra 2 Slope
Lecture Description
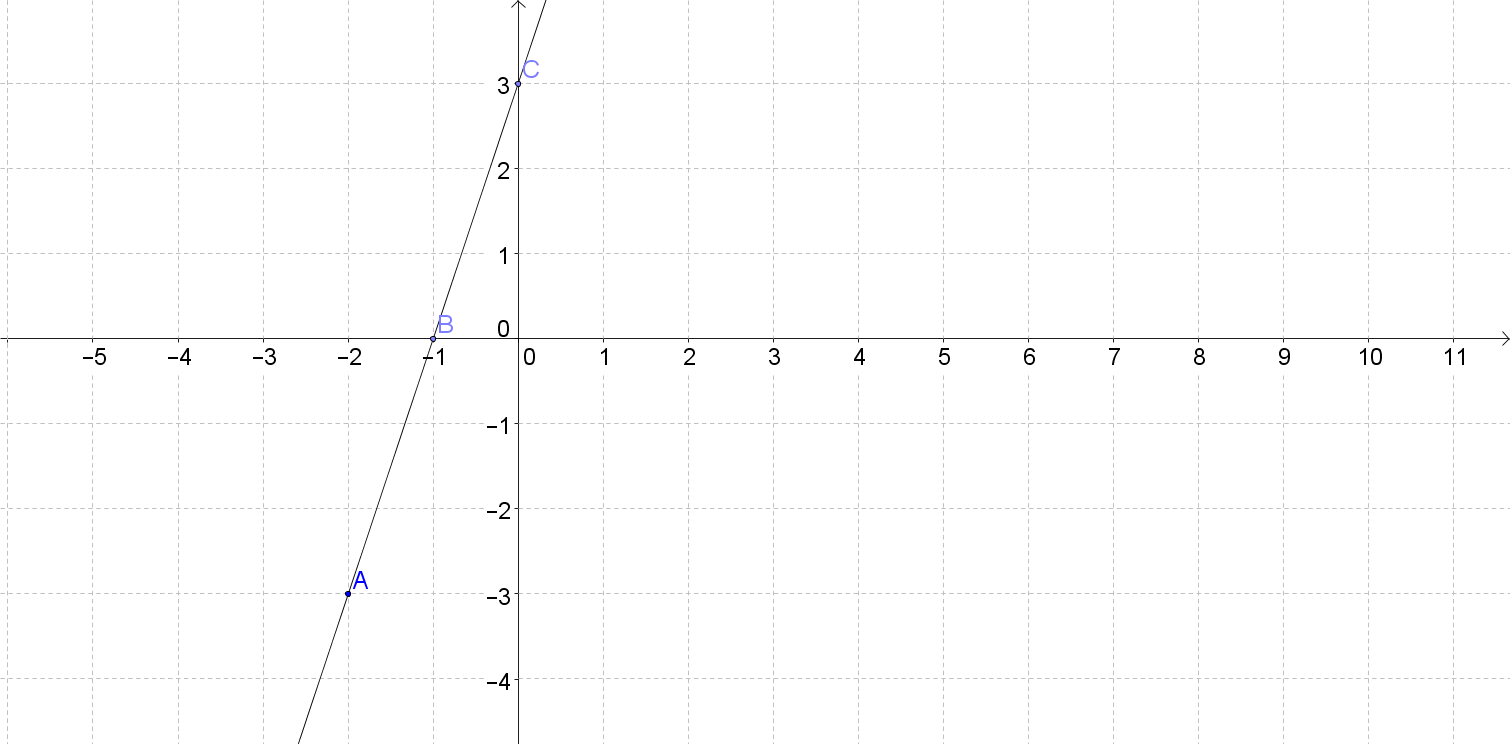
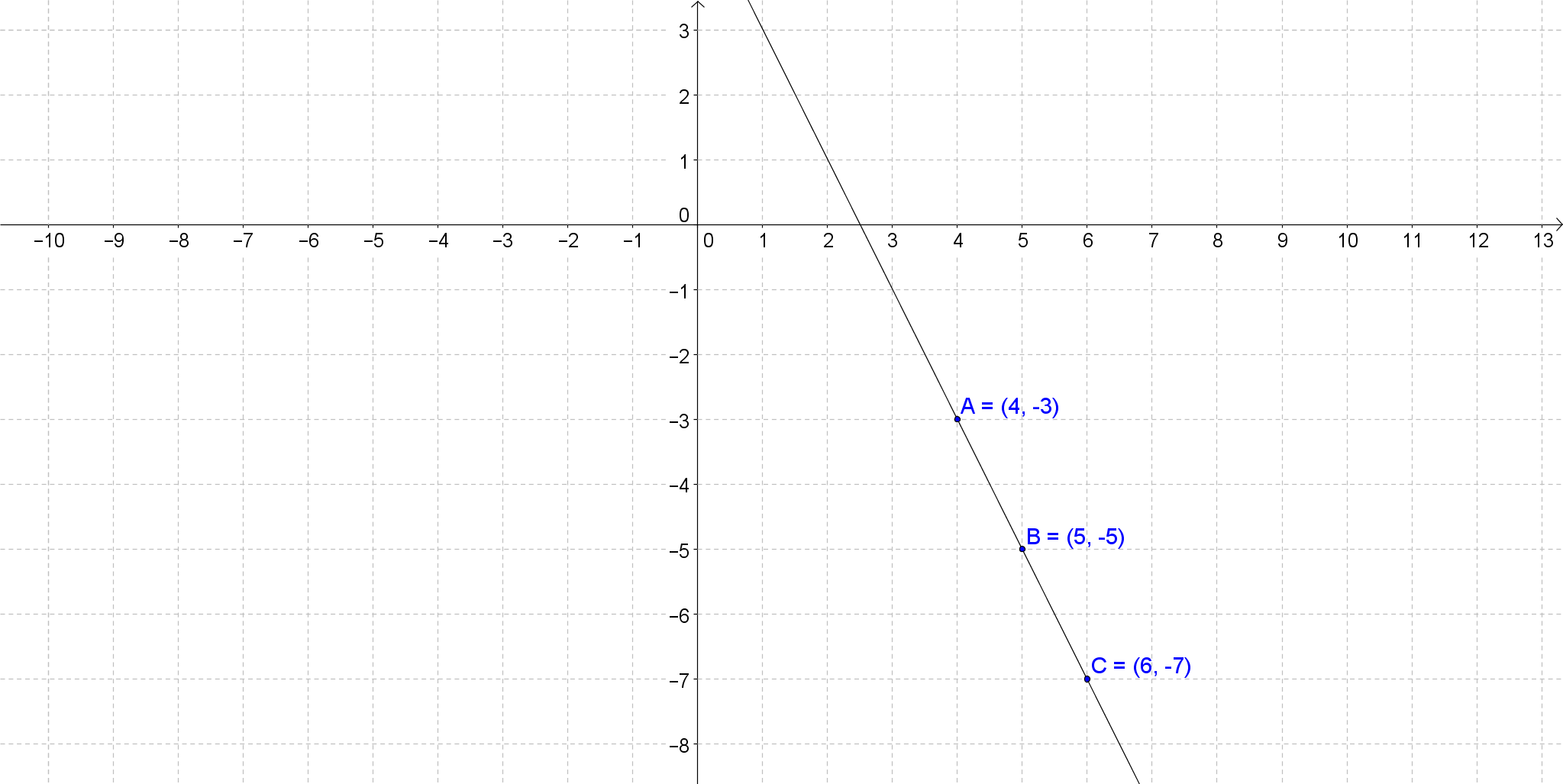
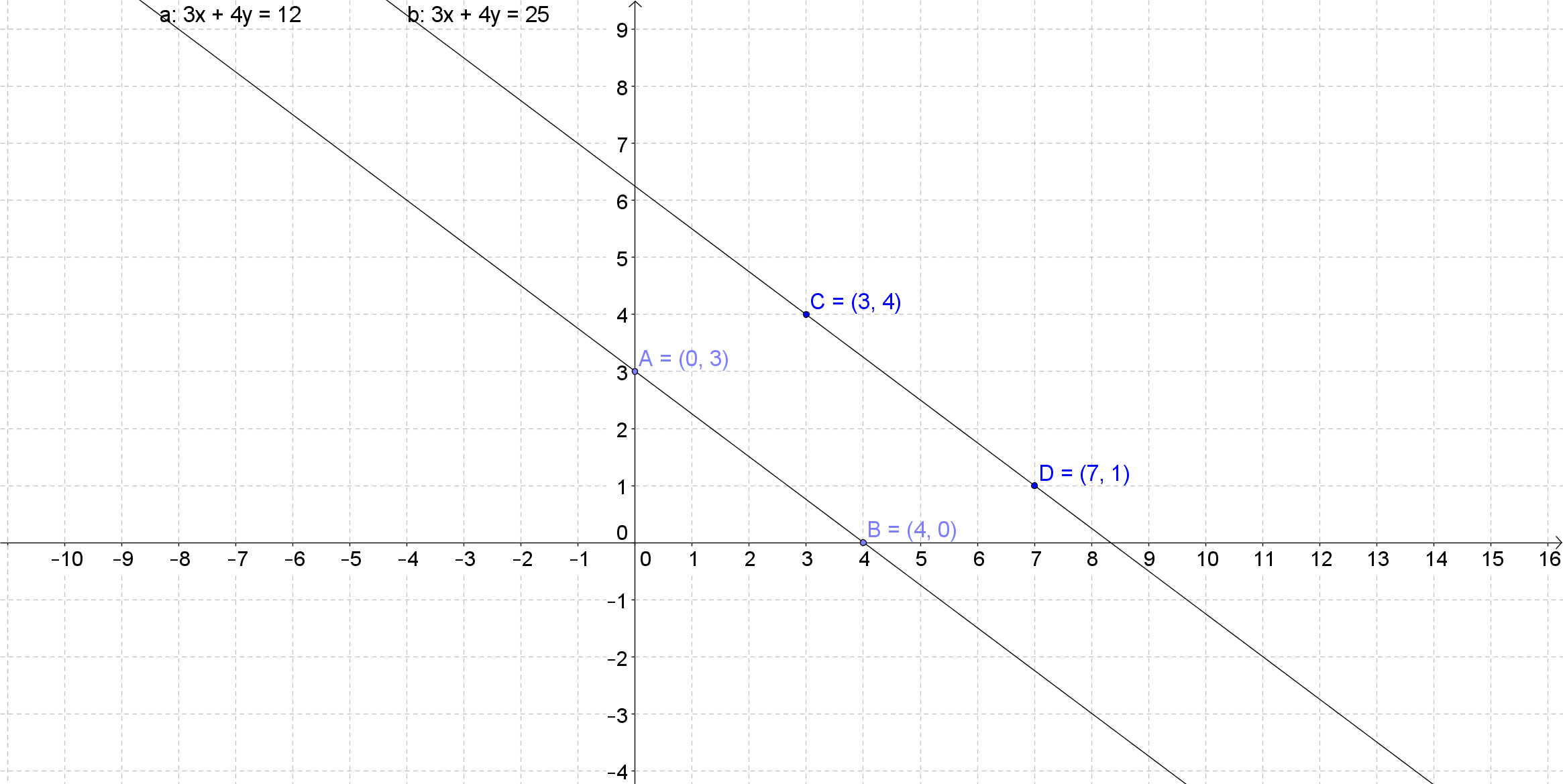
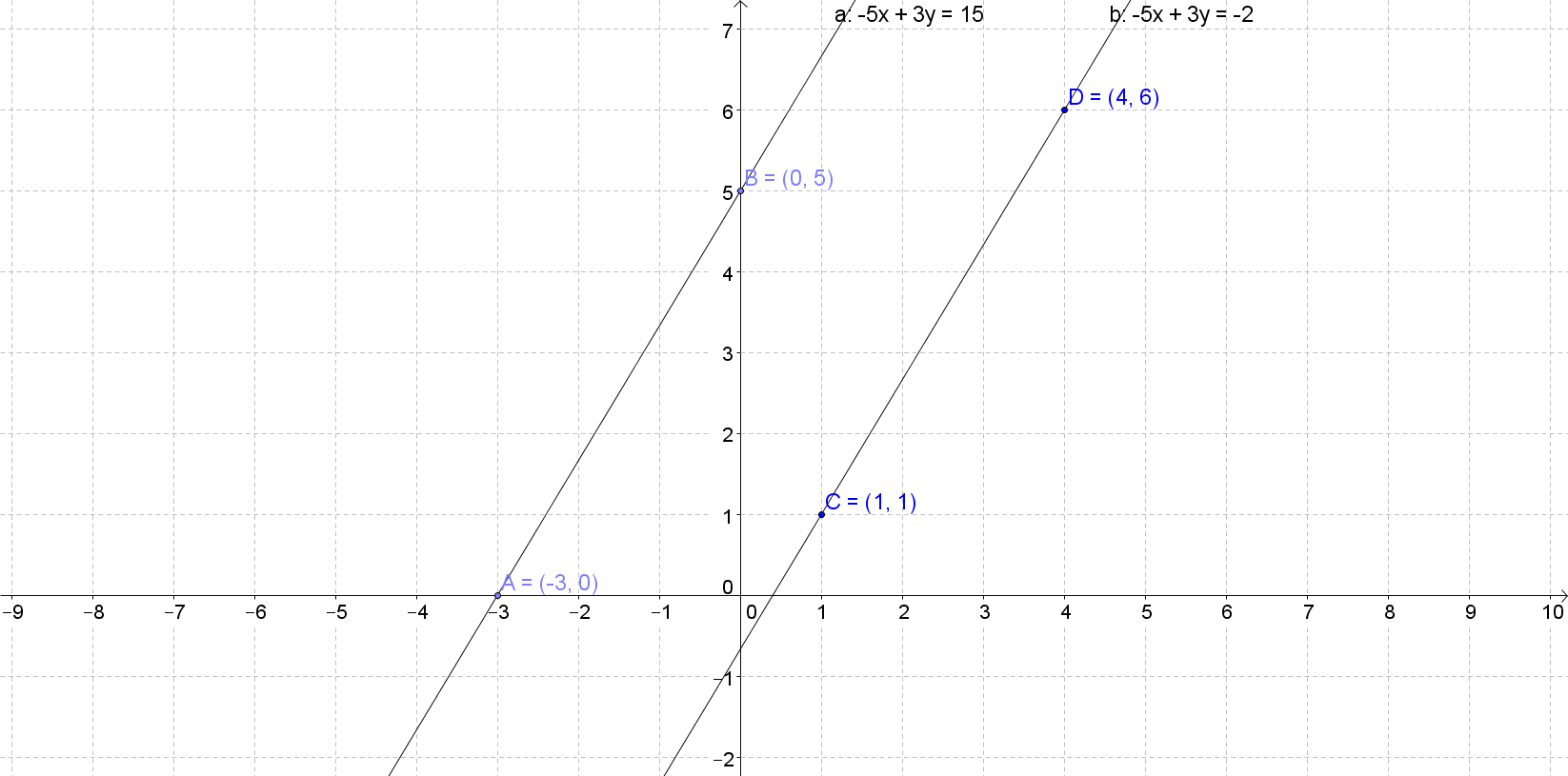
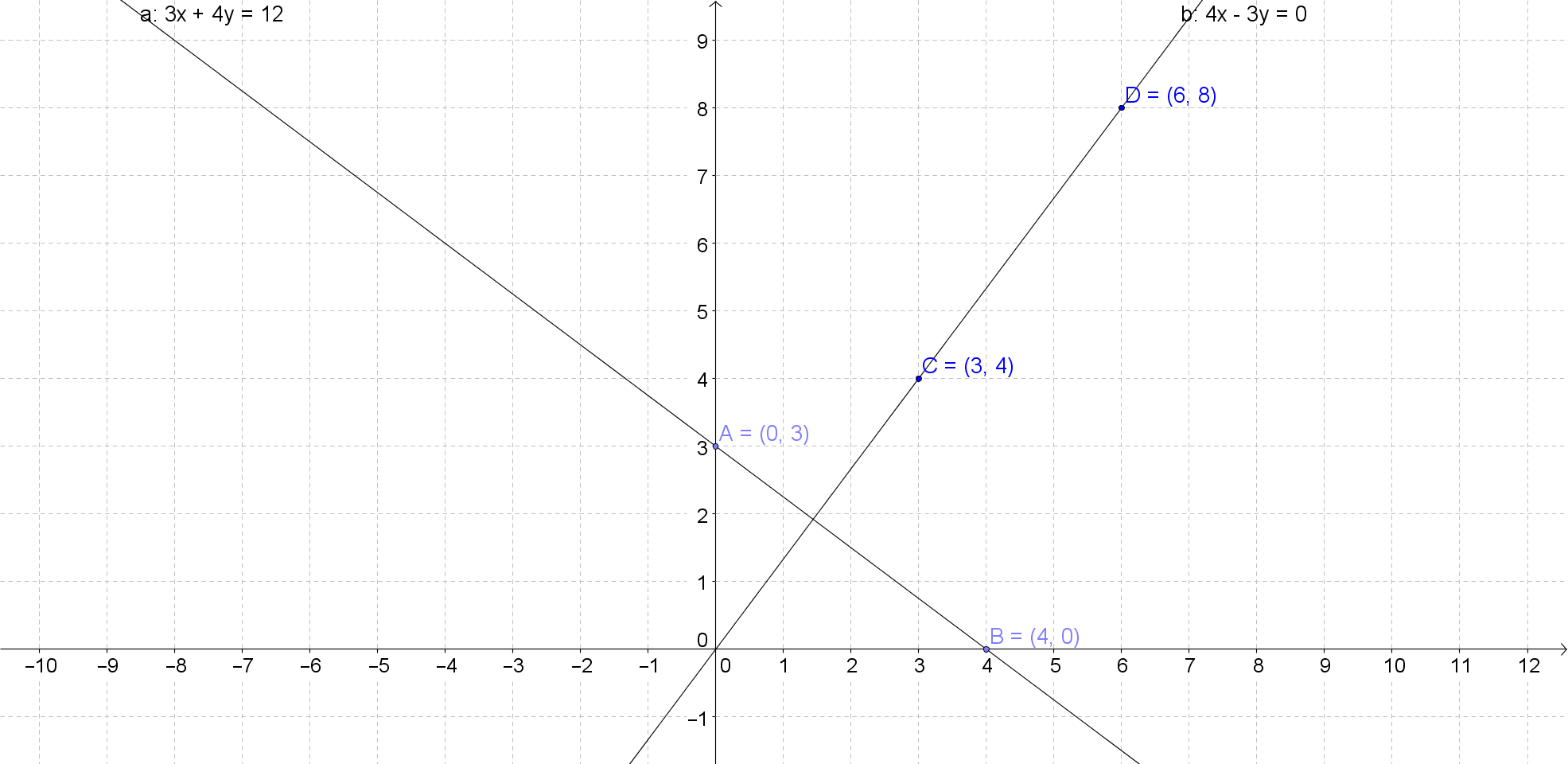
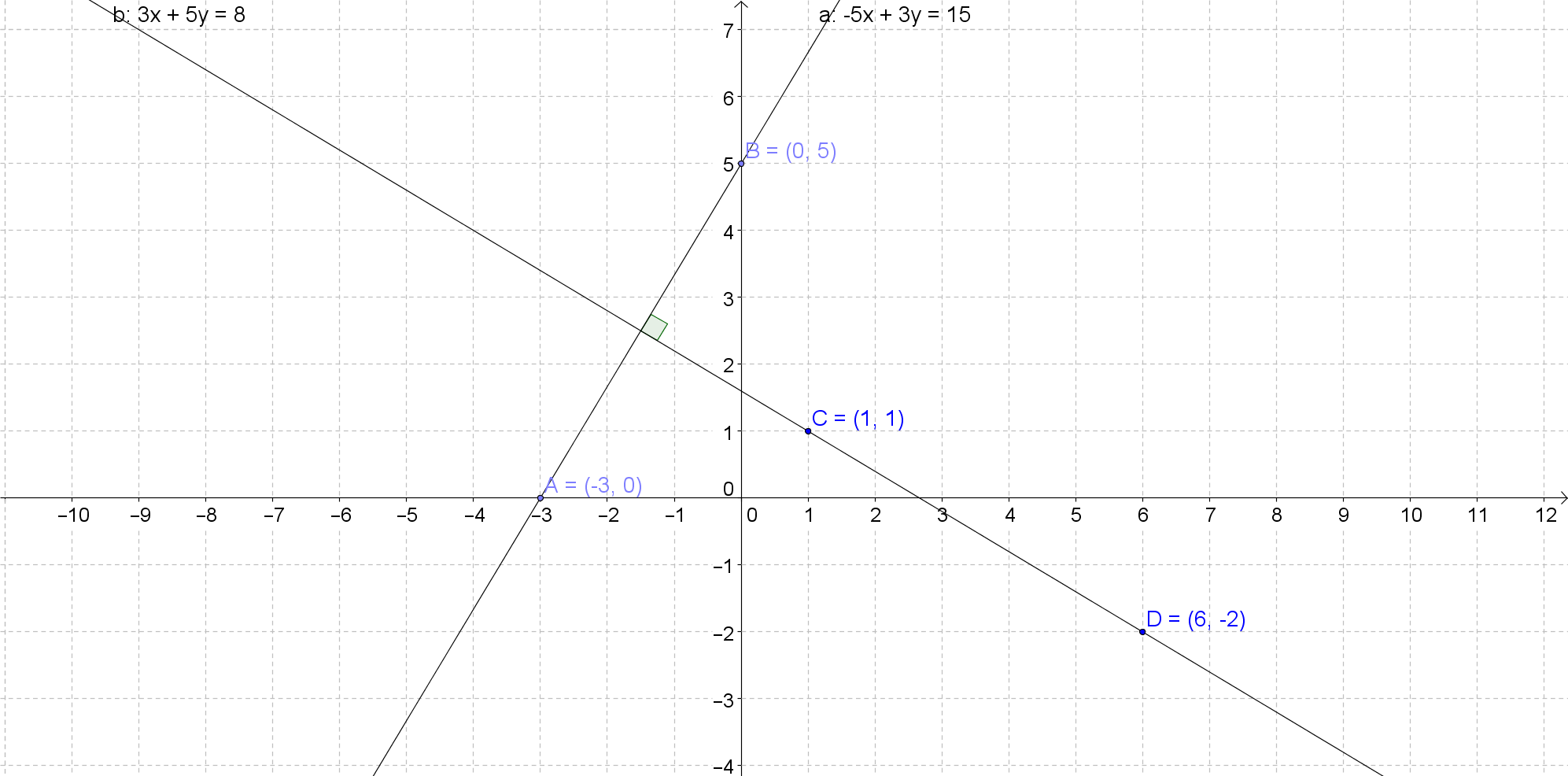
A slope describes the direction and measures how steep a line on a graph is. In a linear equation, y=mx+b, m represents the slope. There are 4 directions of a line: horizontal (parallel to the x-axis), vertical (parallel to the y-axis), increasing or decreasing. The direction is represented as 0 on a linear equation if horizontal and if vertical, the slope is undefined as there is no slope. This lecture also covers the slopes of parallel and perpendicular lines. Parallel lines have the same slope while the product of slopes of two perpendicular lines is equal to -1.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture









































 Carleen Eaton
Carleen Eaton Grant Fraser
Grant Fraser
 Answer Engine
Answer Engine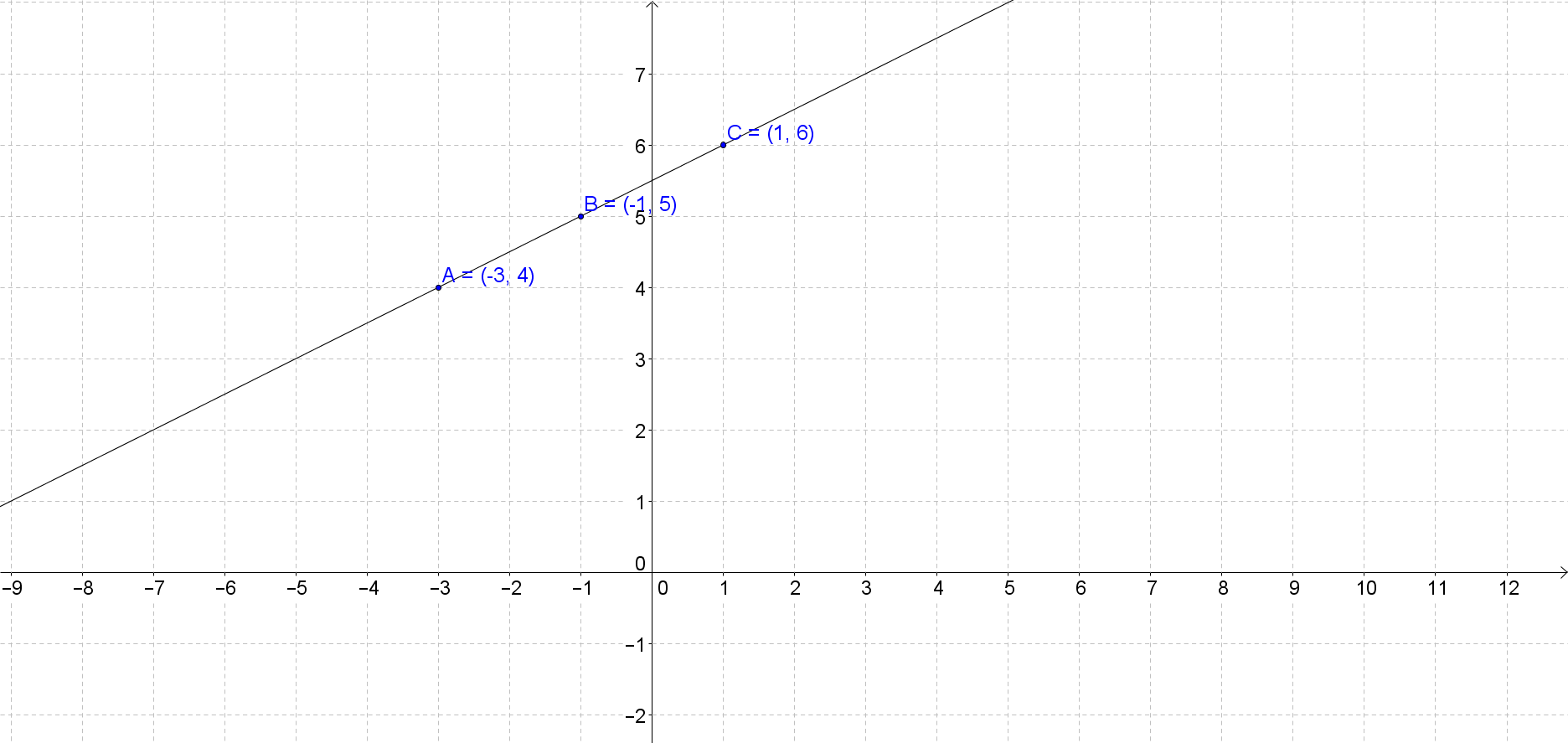




1 answer
Sat Jul 12, 2014 1:33 PM
Post by Matthew Johnston on June 26, 2014
You could just switch the numerator and denominator and make it negative right?
2 answers
Last reply by: Hong Yang
Tue Sep 10, 2019 4:27 PM
Post by abdulaziz bagabas on February 2, 2014
when asked to graph poiny passing through (1,-3) and parallel to the graph of 2x-3y, you should have put the the point on 3 not on 4, or if i am not right can anybody correct me
0 answers
Post by abdulaziz bagabas on February 2, 2014
i really was benefited and entertained by this useful lecture and i would like to thank educator.com team and DR.CARLEEN EATON for those huge efforts to presenting useful lectures.
1 answer
Sat Apr 27, 2013 1:27 PM
Post by Iris Kim on April 6, 2013
You said that vertical lines and lines with the same slope can be parallel. What about two horizontal lines? Can't they be parallel?
1 answer
Fri Oct 26, 2012 11:07 PM
Post by michelle morris on October 24, 2012
Were doing that in school but were also doing standard form w/t form slopes.
also the slope intercept form of an equation , and then writing the slope intercept form given the slope and y-intercept. I dont understand that
2 answers
Last reply by: Justin Wright
Tue Sep 18, 2012 6:51 PM
Post by Sayaka Carpenter on July 14, 2012
wouldn't two horizontal lines be considered parallel as well? you only mentioned vertical and lines with the same slope.
1 answer
Tue Jul 3, 2012 7:15 PM
Post by Vita Kravchenya on June 25, 2012
How many feet in the vertical direction correspond to 10ft in the horizontal direction
one side of triangular 3 ft and other 12 feet