Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Algebra 2
For more information, please see full course syllabus of Algebra 2
Algebra 2 Graphing Inequalities
Lecture Description
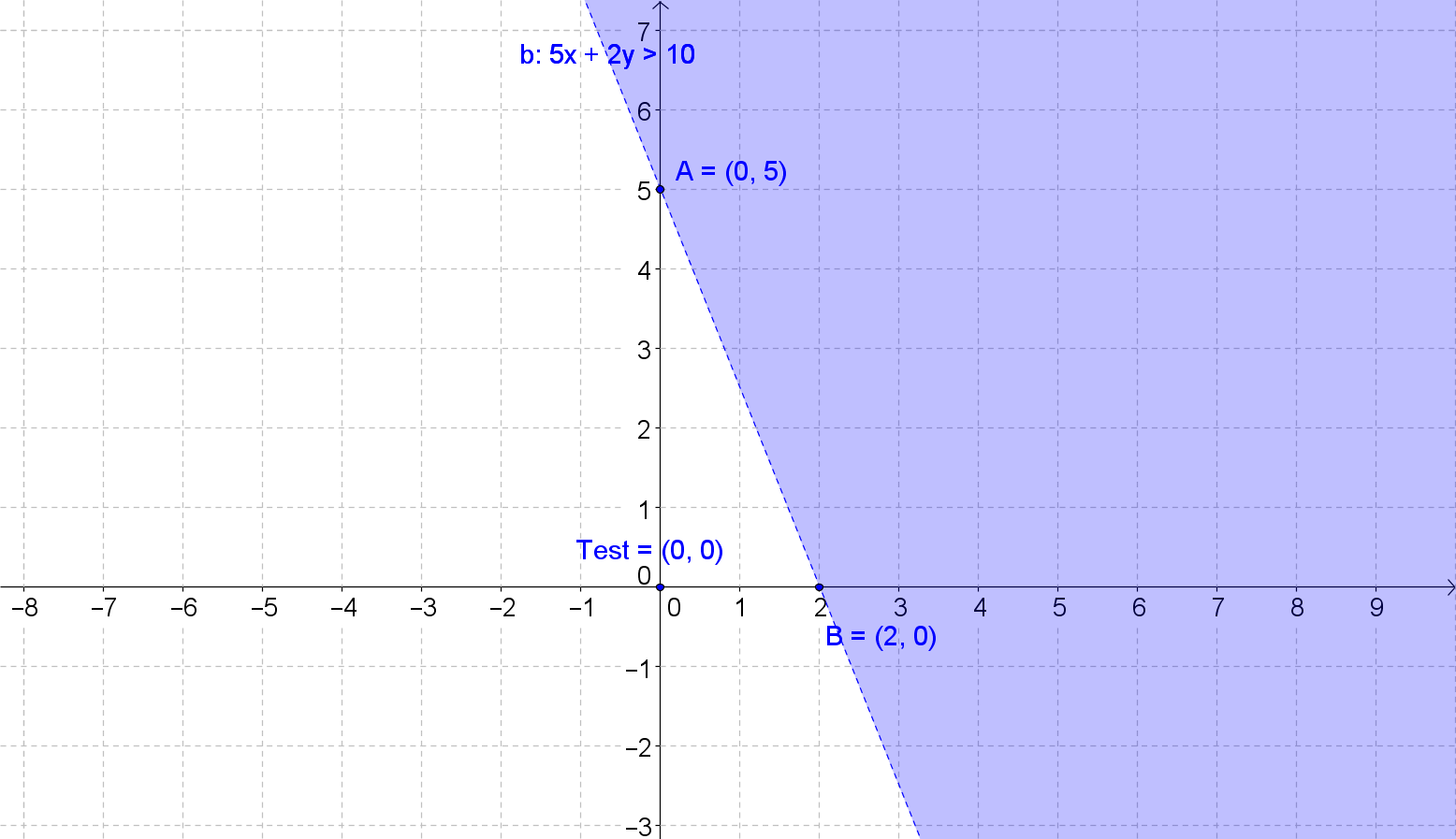
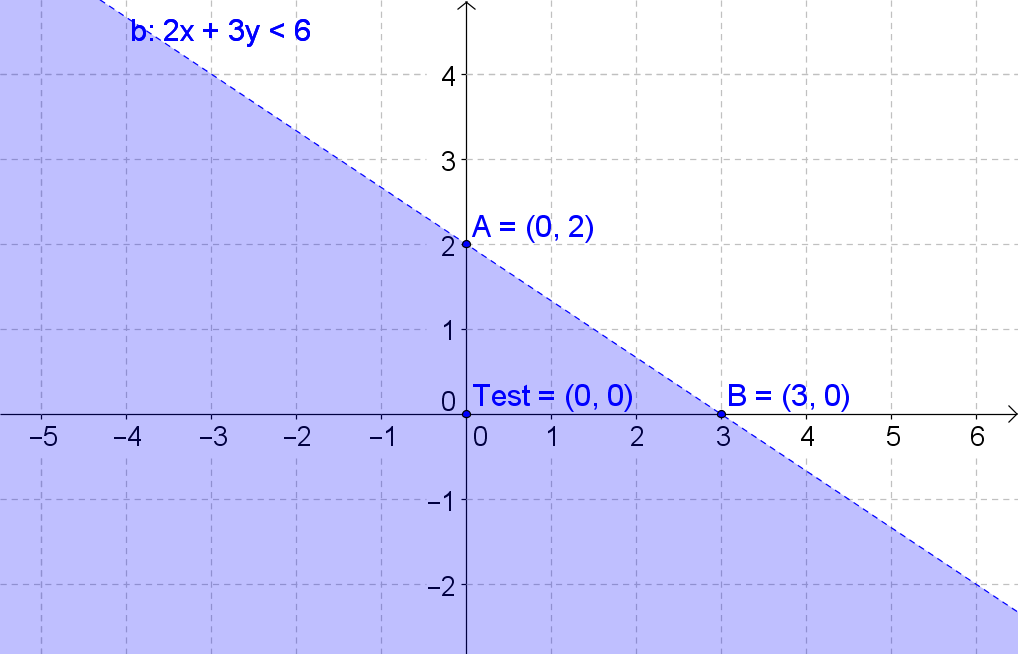
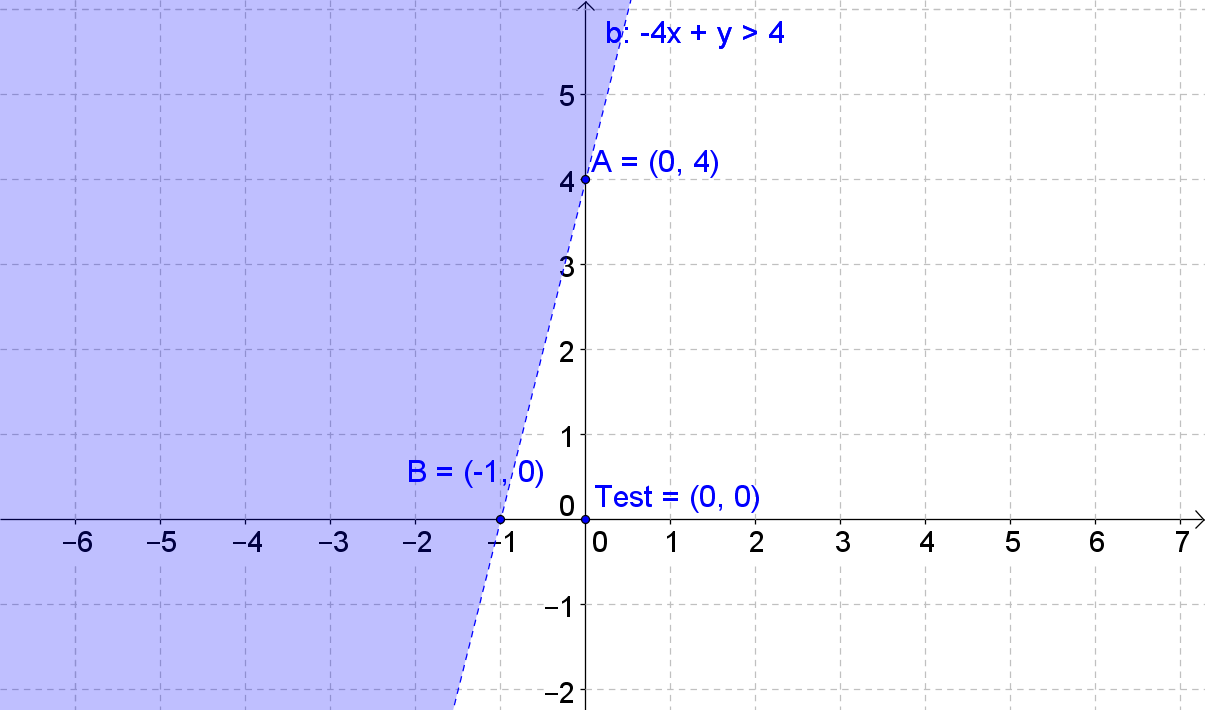
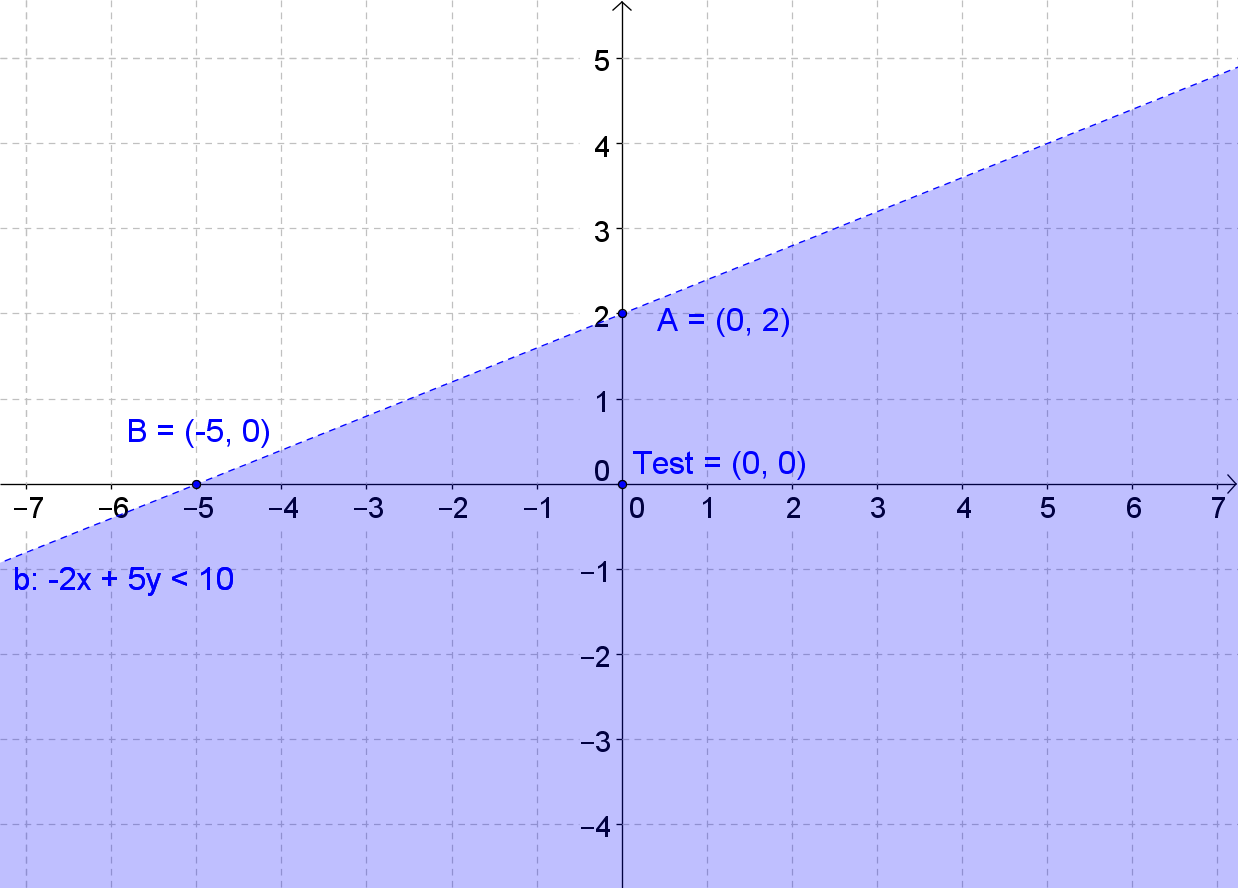
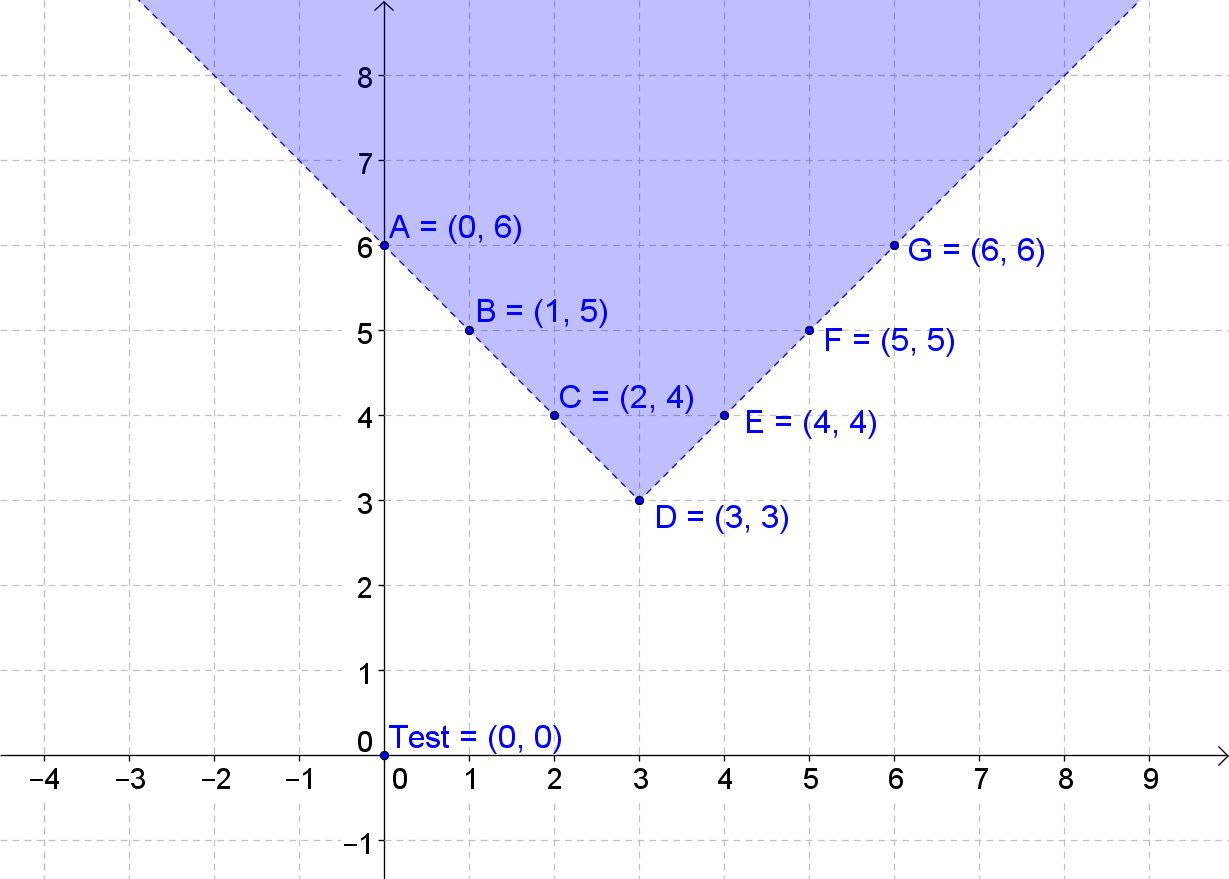
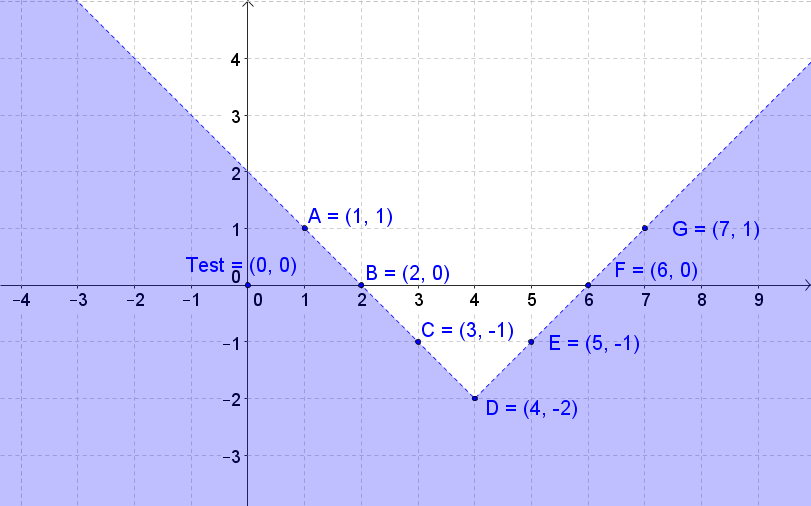
The graph of a linear inequality is a shaded region in the coordinate plane. The boundary of the region is a straight line which is the graph of the corresponding linear function. Sometimes the boundary is a part of the solution, and sometimes it's not. To know which region to shade, you can use a test point. Graphing absolute value inequalities is similar to graphing linear inequalities. Again, we have the corresponding equations that need to be graphed first. After that, we use a test point to determine the half-plane containing the solution set for the inequality. The given examples will allow you to master graphing the inequalities.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture









































 Carleen Eaton
Carleen Eaton Grant Fraser
Grant Fraser
 Answer Engine
Answer Engine




1 answer
Fri Jun 8, 2018 11:42 PM
Post by Krishna vempati on June 8, 2018
At about 3:19 into the lecture one of the coordinate points was incorrectly graphed at (1,0) rather than (1,1). I am really enjoying your course program. Thanks,
1 answer
Last reply by: Magdy Mettias
Sun Sep 23, 2012 3:35 PM
Post by Nancy Dempsey on March 18, 2011
Thanks
0 answers
Post by Jeff Mitchell on March 5, 2011
At about 3:19 into the lecture one of the coordinate points was incorrectly graphed at (1,0) rather than (1,1). I am really enjoying your course program. Thanks,