Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Algebra 2
For more information, please see full course syllabus of Algebra 2
Algebra 2 Square Root Functions and Inequalities
Lecture Description
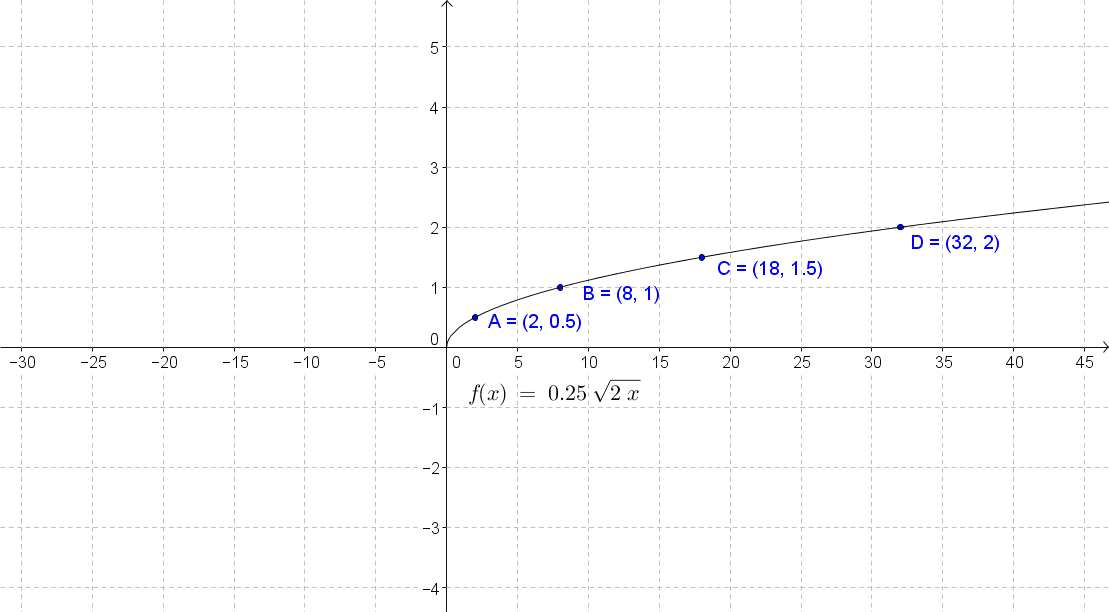
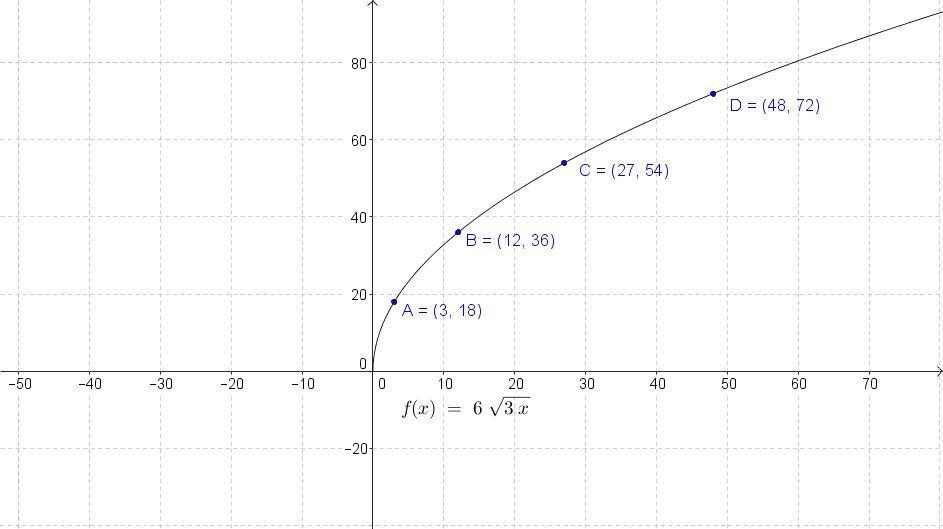
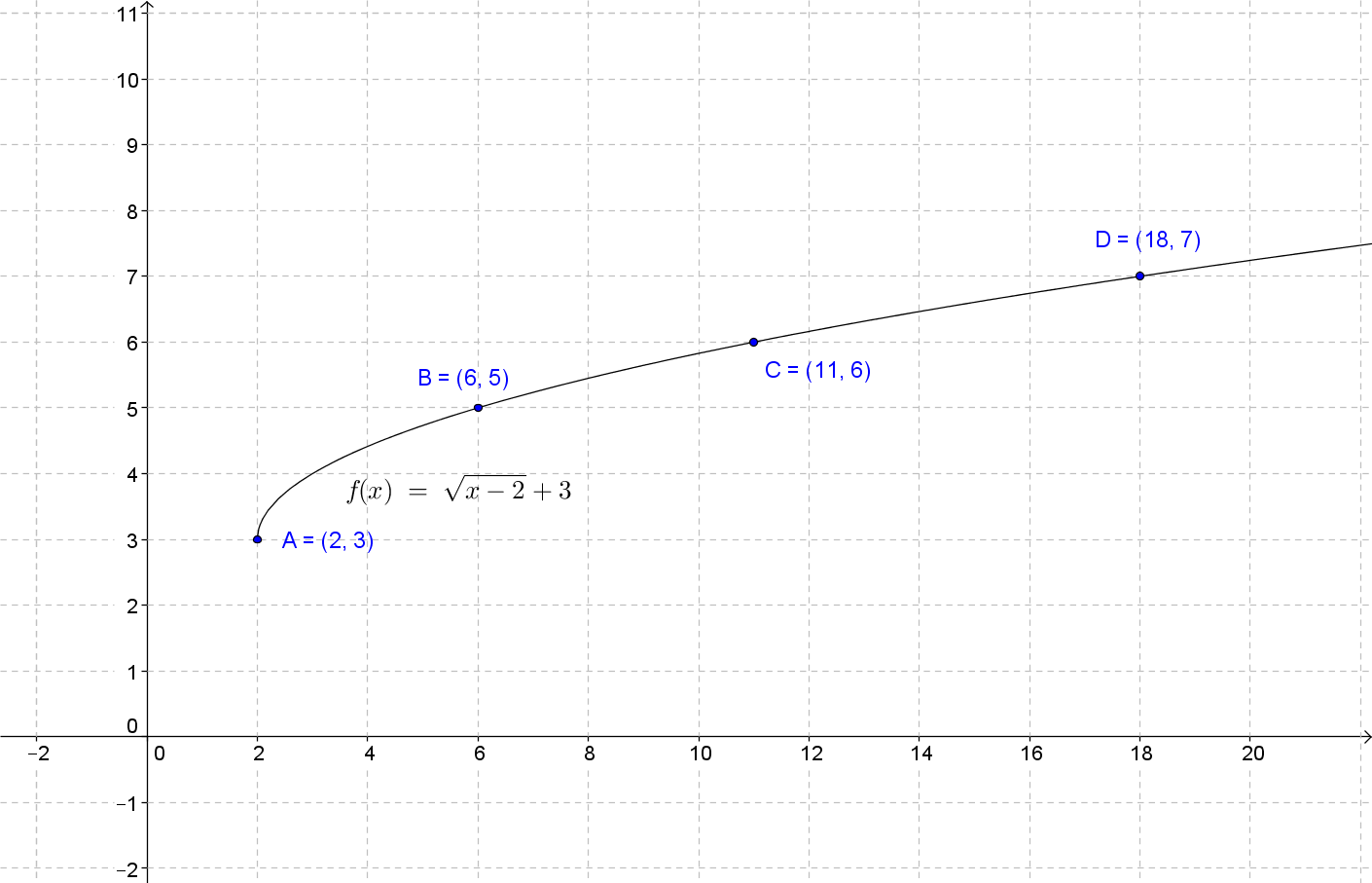
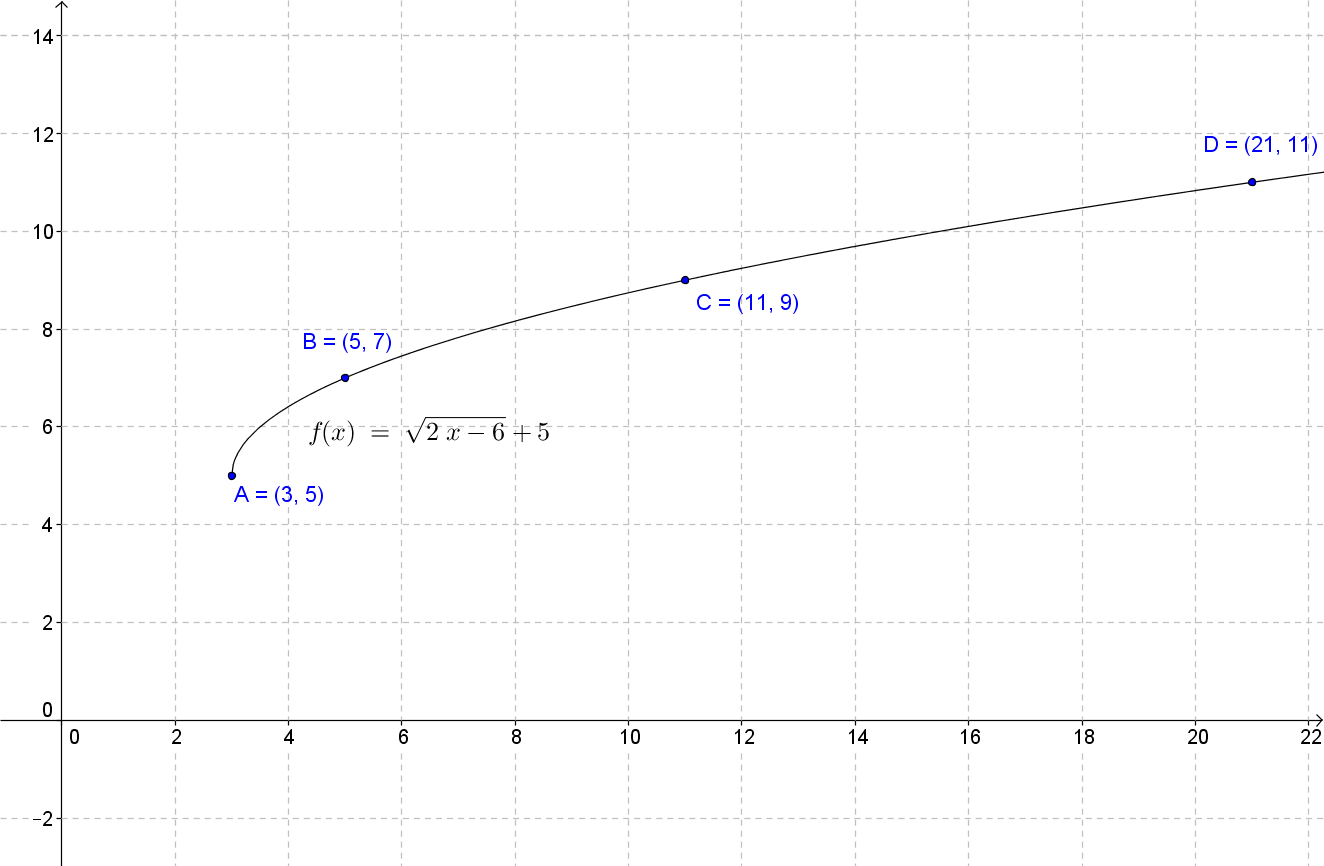
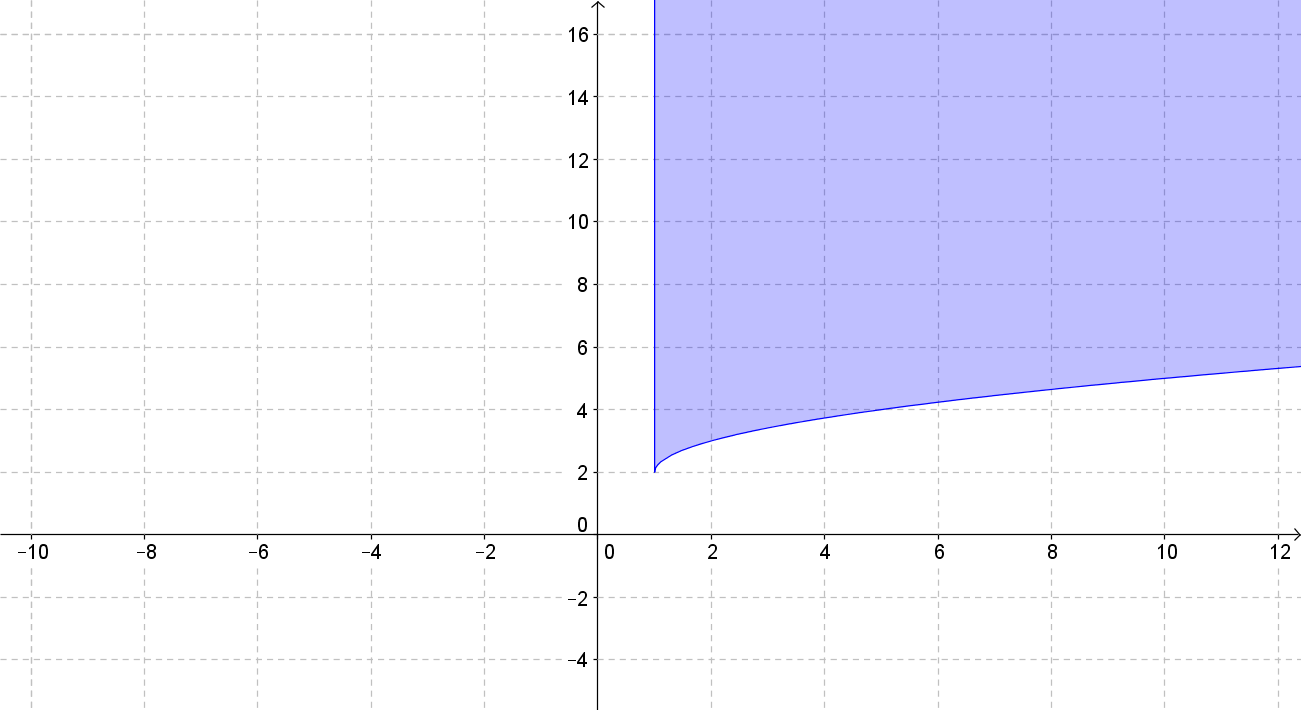
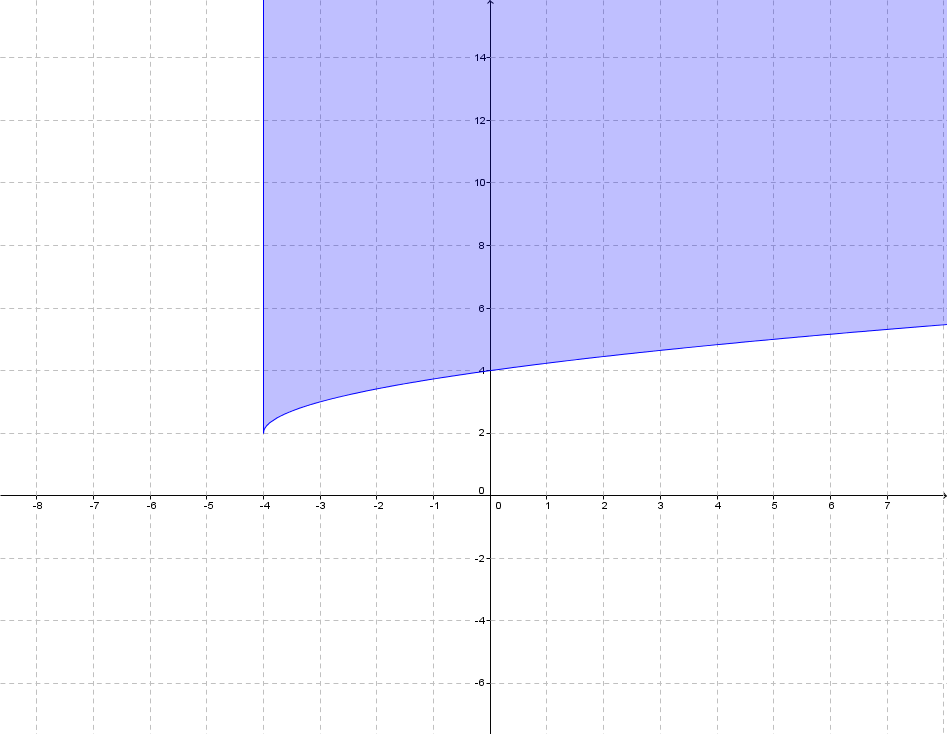
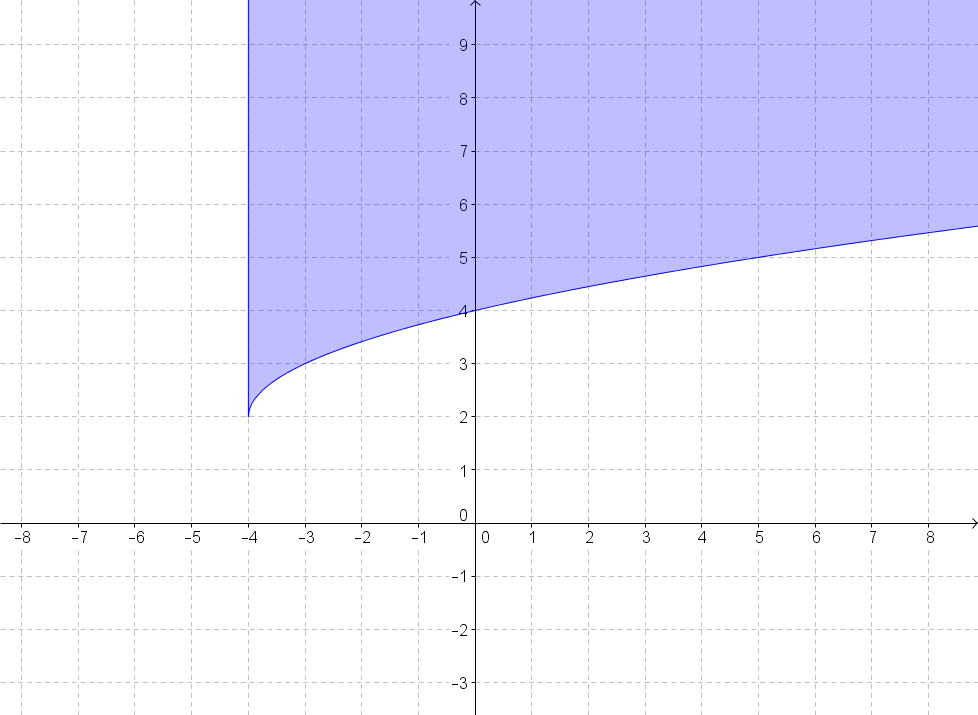
A square root function contains a square root involving a variable and there are some restrictions to the variable under the square root. The radicand must always be positive or equal to zero, which means that the domain of the square root function is restricted to values that make the radicand non-negative. The graph of a square root function is half of a parabola and you'll learn how to graph it in this lecture. Graphing square root inequalities is closely related to graphing the square root functions. We use the same techniques that were used to graph linear and quadratic inequalities, but with an extra step that you'll see in the video.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture









































 Carleen Eaton
Carleen Eaton Grant Fraser
Grant Fraser
 Answer Engine
Answer Engine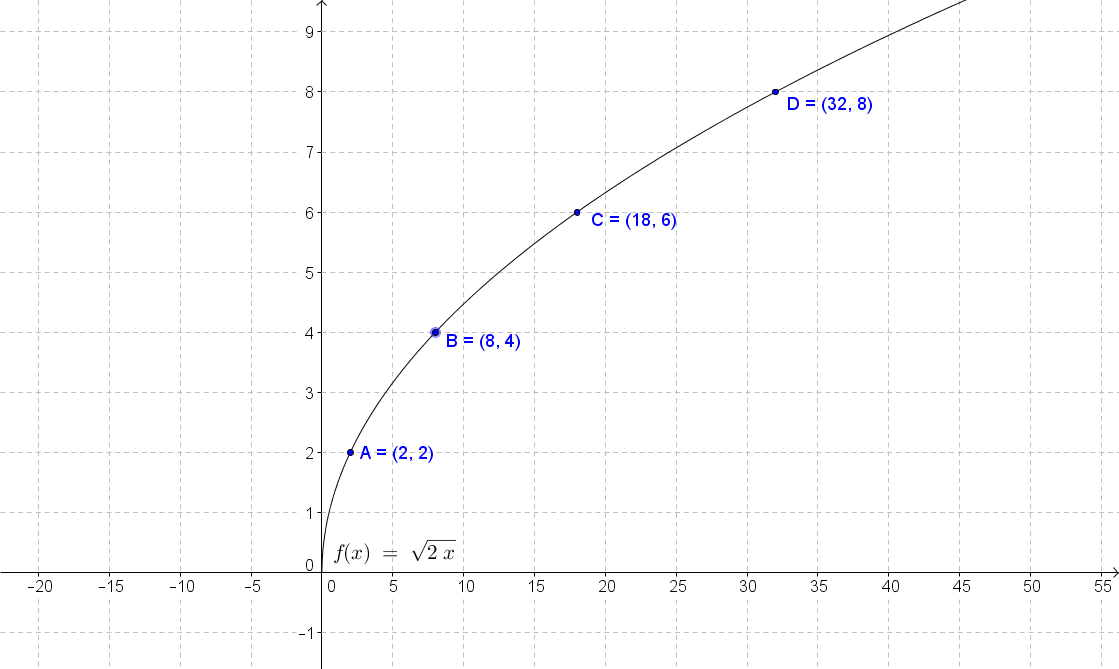




Start Learning Now
Our free lessons will get you started (Adobe Flash® required).
Sign up for Educator.comGet immediate access to our entire library.
Membership Overview