Home » Mathematics » Geometry » Geometric Probability

Mary Pyo

Mary Pyo

Geometric Probability

Slide Duration:

Table of Contents

Section 1: Tools of Geometry
Coordinate Plane

16m 41s

Intro
0:00
The Coordinate System
0:12
Coordinate Plane: X-axis and Y-axis
0:15
Quadrants
1:02
Origin
2:00
Ordered Pair
2:17
Coordinate Plane
2:59
Example: Writing Coordinates
3:01
Coordinate Plane, cont.
4:15
Example: Graphing & Coordinate Plane
4:17
Collinear
5:58
Extra Example 1: Writing Coordinates & Quadrants
7:34
Extra Example 2: Quadrants
8:52
Extra Example 3: Graphing & Coordinate Plane
10:58
Extra Example 4: Collinear
12:50
Points, Lines and Planes

17m 17s

Intro
0:00
Points
0:07
Definition and Example of Points
0:09
Lines
0:50
Definition and Example of Lines
0:51
Planes
2:59
Definition and Example of Planes
3:00
Drawing and Labeling
4:40
Example 1: Drawing and Labeling
4:41
Example 2: Drawing and Labeling
5:54
Example 3: Drawing and Labeling
6:41
Example 4: Drawing and Labeling
8:23
Extra Example 1: Points, Lines and Planes
10:19
Extra Example 2: Naming Figures
11:16
Extra Example 3: Points, Lines and Planes
12:35
Extra Example 4: Draw and Label
14:44
Measuring Segments

31m 31s

Intro
0:00
Segments
0:06
Examples of Segments
0:08
Ruler Postulate
1:30
Ruler Postulate
1:31
Segment Addition Postulate
5:02
Example and Definition of Segment Addition Postulate
5:03
Segment Addition Postulate
8:01
Example 1: Segment Addition Postulate
8:04
Example 2: Segment Addition Postulate
11:15
Pythagorean Theorem
12:36
Definition of Pythagorean Theorem
12:37
Pythagorean Theorem, cont.
15:49
Example: Pythagorean Theorem
15:50
Distance Formula
16:48
Example and Definition of Distance Formula
16:49
Extra Example 1: Find Each Measure
20:32
Extra Example 2: Find the Missing Measure
22:11
Extra Example 3: Find the Distance Between the Two Points
25:36
Extra Example 4: Pythagorean Theorem
29:33
Midpoints and Segment Congruence

42m 26s

Intro
0:00
Definition of Midpoint
0:07
Midpoint
0:10
Midpoint Formulas
1:30
Midpoint Formula: On a Number Line
1:45
Midpoint Formula: In a Coordinate Plane
2:50
Midpoint
4:40
Example: Midpoint on a Number Line
4:43
Midpoint
6:05
Example: Midpoint in a Coordinate Plane
6:06
Midpoint
8:28
Example 1
8:30
Example 2
13:01
Segment Bisector
15:14
Definition and Example of Segment Bisector
15:15
Proofs
17:27
Theorem
17:53
Proof
18:21
Midpoint Theorem
19:37
Example: Proof & Midpoint Theorem
19:38
Extra Example 1: Midpoint on a Number Line
23:44
Extra Example 2: Drawing Diagrams
26:25
Extra Example 3: Midpoint
29:14
Extra Example 4: Segment Bisector
33:21
Angles

42m 34s

Intro
0:00
Angles
0:05
Angle
0:07
Ray
0:23
Opposite Rays
2:09
Angles
3:22
Example: Naming Angle
3:23
Angles
6:39
Interior, Exterior, Angle
6:40
Measure and Degrees
7:38
Protractor Postulate
8:37
Example: Protractor Postulate
8:38
Angle Addition Postulate
11:41
Example: Angle addition Postulate
11:42
Classifying Angles
14:10
Acute Angle
14:16
Right Angles
14:30
Obtuse Angle
14:41
Angle Bisector
15:02
Example: Angle Bisector
15:04
Angle Relationships
16:43
Adjacent Angles
16:47
Vertical Angles
17:49
Linear Pair
19:40
Angle Relationships
20:31
Right Angles
20:32
Supplementary Angles
21:15
Complementary Angles
21:33
Extra Example 1: Angles
24:08
Extra Example 2: Angles
29:06
Extra Example 3: Angles
32:05
Extra Example 4 Angles
35:44
Section 2: Reasoning & Proof
Inductive Reasoning

19m

Intro
0:00
Inductive Reasoning
0:05
Conjecture
0:06
Inductive Reasoning
0:15
Examples
0:55
Example: Sequence
0:56
More Example: Sequence
2:00
Using Inductive Reasoning
2:50
Example: Conjecture
2:51
More Example: Conjecture
3:48
Counterexamples
4:56
Counterexample
4:58
Extra Example 1: Conjecture
6:59
Extra Example 2: Sequence and Pattern
10:20
Extra Example 3: Inductive Reasoning
12:46
Extra Example 4: Conjecture and Counterexample
15:17
Conditional Statements

42m 47s

Intro
0:00
If Then Statements
0:05
If Then Statements
0:06
Other Forms
2:29
Example: Without Then
2:40
Example: Using When
3:03
Example: Hypothesis
3:24
Identify the Hypothesis and Conclusion
3:52
Example 1: Hypothesis and Conclusion
3:58
Example 2: Hypothesis and Conclusion
4:31
Example 3: Hypothesis and Conclusion
5:38
Write in If Then Form
6:16
Example 1: Write in If Then Form
6:23
Example 2: Write in If Then Form
6:57
Example 3: Write in If Then Form
7:39
Other Statements
8:40
Other Statements
8:41
Converse Statements
9:18
Converse Statements
9:20
Converses and Counterexamples
11:04
Converses and Counterexamples
11:05
Example 1: Converses and Counterexamples
12:02
Example 2: Converses and Counterexamples
15:10
Example 3: Converses and Counterexamples
17:08
Inverse Statement
19:58
Definition and Example
19:59
Inverse Statement
21:46
Example 1: Inverse and Counterexample
21:47
Example 2: Inverse and Counterexample
23:34
Contrapositive Statement
25:20
Definition and Example
25:21
Contrapositive Statement
26:58
Example: Contrapositive Statement
27:00
Summary
29:03
Summary of Lesson
29:04
Extra Example 1: Hypothesis and Conclusion
32:20
Extra Example 2: If-Then Form
33:23
Extra Example 3: Converse, Inverse, and Contrapositive
34:54
Extra Example 4: Converse, Inverse, and Contrapositive
37:56
Point, Line, and Plane Postulates

17m 24s

Intro
0:00
What are Postulates?
0:09
Definition of Postulates
0:10
Postulates
1:22
Postulate 1: Two Points
1:23
Postulate 2: Three Points
2:02
Postulate 3: Line
2:45
Postulates, cont..
3:08
Postulate 4: Plane
3:09
Postulate 5: Two Points in a Plane
3:53
Postulates, cont..
4:46
Postulate 6: Two Lines Intersect
4:47
Postulate 7: Two Plane Intersect
5:28
Using the Postulates
6:34
Examples: True or False
6:35
Using the Postulates
10:18
Examples: True or False
10:19
Extra Example 1: Always, Sometimes, or Never
12:22
Extra Example 2: Always, Sometimes, or Never
13:15
Extra Example 3: Always, Sometimes, or Never
14:16
Extra Example 4: Always, Sometimes, or Never
15:03
Deductive Reasoning

36m 3s

Intro
0:00
Deductive Reasoning
0:06
Definition of Deductive Reasoning
0:07
Inductive vs. Deductive
2:51
Inductive Reasoning
2:52
Deductive reasoning
3:19
Law of Detachment
3:47
Law of Detachment
3:48
Examples of Law of Detachment
4:31
Law of Syllogism
7:32
Law of Syllogism
7:33
Example 1: Making a Conclusion
9:02
Example 2: Making a Conclusion
12:54
Using Laws of Logic
14:12
Example 1: Determine the Logic
14:42
Example 2: Determine the Logic
17:02
Using Laws of Logic, cont.
18:47
Example 3: Determine the Logic
19:03
Example 4: Determine the Logic
20:56
Extra Example 1: Determine the Conclusion and Law
22:12
Extra Example 2: Determine the Conclusion and Law
25:39
Extra Example 3: Determine the Logic and Law
29:50
Extra Example 4: Determine the Logic and Law
31:27
Proofs in Algebra: Properties of Equality

44m 31s

Intro
0:00
Properties of Equality
0:10
Addition Property of Equality
0:28
Subtraction Property of Equality
1:10
Multiplication Property of Equality
1:41
Division Property of Equality
1:55
Addition Property of Equality Using Angles
2:46
Properties of Equality, cont.
4:10
Reflexive Property of Equality
4:11
Symmetric Property of Equality
5:24
Transitive Property of Equality
6:10
Properties of Equality, cont.
7:04
Substitution Property of Equality
7:05
Distributive Property of Equality
8:34
Two Column Proof
9:40
Example: Two Column Proof
9:46
Proof Example 1
16:13
Proof Example 2
23:49
Proof Example 3
30:33
Extra Example 1: Name the Property of Equality
38:07
Extra Example 2: Name the Property of Equality
40:16
Extra Example 3: Name the Property of Equality
41:35
Extra Example 4: Name the Property of Equality
43:02
Proving Segment Relationship

41m 2s

Intro
0:00
Good Proofs
0:12
Five Essential Parts
0:13
Proof Reasons
1:38
Undefined
1:40
Definitions
2:06
Postulates
2:42
Previously Proven Theorems
3:24
Congruence of Segments
4:10
Theorem: Congruence of Segments
4:12
Proof Example
10:16
Proof: Congruence of Segments
10:17
Setting Up Proofs
19:13
Example: Two Segments with Equal Measures
19:15
Setting Up Proofs
21:48
Example: Vertical Angles are Congruent
21:50
Setting Up Proofs
23:59
Example: Segment of a Triangle
24:00
Extra Example 1: Congruence of Segments
27:03
Extra Example 2: Setting Up Proofs
28:50
Extra Example 3: Setting Up Proofs
30:55
Extra Example 4: Two-Column Proof
33:11
Proving Angle Relationships

33m 37s

Intro
0:00
Supplement Theorem
0:05
Supplementary Angles
0:06
Congruence of Angles
2:37
Proof: Congruence of Angles
2:38
Angle Theorems
6:54
Angle Theorem 1: Supplementary Angles
6:55
Angle Theorem 2: Complementary Angles
10:25
Angle Theorems
11:32
Angle Theorem 3: Right Angles
11:35
Angle Theorem 4: Vertical Angles
12:09
Angle Theorem 5: Perpendicular Lines
12:57
Using Angle Theorems
13:45
Example 1: Always, Sometimes, or Never
13:50
Example 2: Always, Sometimes, or Never
14:28
Example 3: Always, Sometimes, or Never
16:21
Extra Example 1: Always, Sometimes, or Never
16:53
Extra Example 2: Find the Measure of Each Angle
18:55
Extra Example 3: Find the Measure of Each Angle
25:03
Extra Example 4: Two-Column Proof
27:08
Section 3: Perpendicular & Parallel Lines
Parallel Lines and Transversals

37m 35s

Intro
0:00
Lines
0:06
Parallel Lines
0:09
Skew Lines
2:02
Transversal
3:42
Angles Formed by a Transversal
4:28
Interior Angles
5:53
Exterior Angles
6:09
Consecutive Interior Angles
7:04
Alternate Exterior Angles
9:47
Alternate Interior Angles
11:22
Corresponding Angles
12:27
Angles Formed by a Transversal
15:29
Relationship Between Angles
15:30
Extra Example 1: Intersecting, Parallel, or Skew
19:26
Extra Example 2: Draw a Diagram
21:37
Extra Example 3: Name the Figures
24:12
Extra Example 4: Angles Formed by a Transversal
28:38
Angles and Parallel Lines

41m 53s

Intro
0:00
Corresponding Angles Postulate
0:05
Corresponding Angles Postulate
0:06
Alternate Interior Angles Theorem
3:05
Alternate Interior Angles Theorem
3:07
Consecutive Interior Angles Theorem
5:16
Consecutive Interior Angles Theorem
5:17
Alternate Exterior Angles Theorem
6:42
Alternate Exterior Angles Theorem
6:43
Parallel Lines Cut by a Transversal
7:18
Example: Parallel Lines Cut by a Transversal
7:19
Perpendicular Transversal Theorem
14:54
Perpendicular Transversal Theorem
14:55
Extra Example 1: State the Postulate or Theorem
16:37
Extra Example 2: Find the Measure of the Numbered Angle
18:53
Extra Example 3: Find the Measure of Each Angle
25:13
Extra Example 4: Find the Values of x, y, and z
36:26
Slope of Lines

44m 6s

Intro
0:00
Definition of Slope
0:06
Slope Equation
0:13
Slope of a Line
3:45
Example: Find the Slope of a Line
3:47
Slope of a Line
8:38
More Example: Find the Slope of a Line
8:40
Slope Postulates
12:32
Proving Slope Postulates
12:33
Parallel or Perpendicular Lines
17:23
Example: Parallel or Perpendicular Lines
17:24
Using Slope Formula
20:02
Example: Using Slope Formula
20:03
Extra Example 1: Slope of a Line
25:10
Extra Example 2: Slope of a Line
26:31
Extra Example 3: Graph the Line
34:11
Extra Example 4: Using the Slope Formula
38:50
Proving Lines Parallel

25m 55s

Intro
0:00
Postulates
0:06
Postulate 1: Parallel Lines
0:21
Postulate 2: Parallel Lines
2:16
Parallel Postulate
3:28
Definition and Example of Parallel Postulate
3:29
Theorems
4:29
Theorem 1: Parallel Lines
4:40
Theorem 2: Parallel Lines
5:37
Theorems, cont.
6:10
Theorem 3: Parallel Lines
6:11
Extra Example 1: Determine Parallel Lines
6:56
Extra Example 2: Find the Value of x
11:42
Extra Example 3: Opposite Sides are Parallel
14:48
Extra Example 4: Proving Parallel Lines
20:42
Parallels and Distance

19m 48s

Intro
0:00
Distance Between a Points and Line
0:07
Definition and Example
0:08
Distance Between Parallel Lines
1:51
Definition and Example
1:52
Extra Example 1: Drawing a Segment to Represent Distance
3:02
Extra Example 2: Drawing a Segment to Represent Distance
4:27
Extra Example 3: Graph, Plot, and Construct a Perpendicular Segment
5:13
Extra Example 4: Distance Between Two Parallel Lines
15:37
Section 4: Congruent Triangles
Classifying Triangles

28m 43s

Intro
0:00
Triangles
0:09
Triangle: A Three-Sided Polygon
0:10
Sides
1:00
Vertices
1:22
Angles
1:56
Classifying Triangles by Angles
2:59
Acute Triangle
3:19
Obtuse Triangle
4:08
Right Triangle
4:44
Equiangular Triangle
5:38
Definition and Example of an Equiangular Triangle
5:39
Classifying Triangles by Sides
6:57
Scalene Triangle
7:17
Isosceles Triangle
7:57
Equilateral Triangle
8:12
Isosceles Triangle
8:58
Labeling Isosceles Triangle
9:00
Labeling Right Triangle
10:44
Isosceles Triangle
11:10
Example: Find x, AB, BC, and AC
11:11
Extra Example 1: Classify Each Triangle
13:45
Extra Example 2: Always, Sometimes, or Never
16:28
Extra Example 3: Find All the Sides of the Isosceles Triangle
20:29
Extra Example 4: Distance Formula and Triangle
22:29
Measuring Angles in Triangles

44m 43s

Intro
0:00
Angle Sum Theorem
0:09
Angle Sum Theorem for Triangle
0:11
Using Angle Sum Theorem
4:06
Find the Measure of the Missing Angle
4:07
Third Angle Theorem
4:58
Example: Third Angle Theorem
4:59
Exterior Angle Theorem
7:58
Example: Exterior Angle Theorem
8:00
Flow Proof of Exterior Angle Theorem
15:14
Flow Proof of Exterior Angle Theorem
15:17
Triangle Corollaries
27:21
Triangle Corollary 1
27:50
Triangle Corollary 2
30:42
Extra Example 1: Find the Value of x
32:55
Extra Example 2: Find the Value of x
34:20
Extra Example 3: Find the Measure of the Angle
35:38
Extra Example 4: Find the Measure of Each Numbered Angle
39:00
Exploring Congruent Triangles

26m 46s

Intro
0:00
Congruent Triangles
0:15
Example of Congruent Triangles
0:17
Corresponding Parts
3:39
Corresponding Angles and Sides of Triangles
3:40
Definition of Congruent Triangles
11:24
Definition of Congruent Triangles
11:25
Triangle Congruence
16:37
Congruence of Triangles
16:38
Extra Example 1: Congruence Statement
18:24
Extra Example 2: Congruence Statement
21:26
Extra Example 3: Draw and Label the Figure
23:09
Extra Example 4: Drawing Triangles
24:04
Proving Triangles Congruent

47m 51s

Intro
0:00
SSS Postulate
0:18
Side-Side-Side Postulate
0:27
SAS Postulate
2:26
Side-Angle-Side Postulate
2:29
SAS Postulate
3:57
Proof Example
3:58
ASA Postulate
11:47
Angle-Side-Angle Postulate
11:53
AAS Theorem
14:13
Angle-Angle-Side Theorem
14:14
Methods Overview
16:16
Methods Overview
16:17
SSS
16:33
SAS
17:06
ASA
17:50
AAS
18:17
CPCTC
19:14
Extra Example 1:Proving Triangles are Congruent
21:29
Extra Example 2: Proof
25:40
Extra Example 3: Proof
30:41
Extra Example 4: Proof
38:41
Isosceles and Equilateral Triangles

27m 53s

Intro
0:00
Isosceles Triangle Theorem
0:07
Isosceles Triangle Theorem
0:09
Isosceles Triangle Theorem
2:26
Example: Using the Isosceles Triangle Theorem
2:27
Isosceles Triangle Theorem Converse
3:29
Isosceles Triangle Theorem Converse
3:30
Equilateral Triangle Theorem Corollaries
4:30
Equilateral Triangle Theorem Corollary 1
4:59
Equilateral Triangle Theorem Corollary 2
5:55
Extra Example 1: Find the Value of x
7:08
Extra Example 2: Find the Value of x
10:04
Extra Example 3: Proof
14:04
Extra Example 4: Proof
22:41
Section 5: Triangle Inequalities
Special Segments in Triangles

43m 44s

Intro
0:00
Perpendicular Bisector
0:06
Perpendicular Bisector
0:07
Perpendicular Bisector
4:07
Perpendicular Bisector Theorems
4:08
Median
6:30
Definition of Median
6:31
Median
9:41
Example: Median
9:42
Altitude
12:22
Definition of Altitude
12:23
Angle Bisector
14:33
Definition of Angle Bisector
14:34
Angle Bisector
16:41
Angle Bisector Theorems
16:42
Special Segments Overview
18:57
Perpendicular Bisector
19:04
Median
19:32
Altitude
19:49
Angle Bisector
20:02
Examples: Special Segments
20:18
Extra Example 1: Draw and Label
22:36
Extra Example 2: Draw the Altitudes for Each Triangle
24:37
Extra Example 3: Perpendicular Bisector
27:57
Extra Example 4: Draw, Label, and Write Proof
34:33
Right Triangles

26m 34s

Intro
0:00
LL Theorem
0:21
Leg-Leg Theorem
0:25
HA Theorem
2:23
Hypotenuse-Angle Theorem
2:24
LA Theorem
4:49
Leg-Angle Theorem
4:50
LA Theorem
6:18
Example: Find x and y
6:19
HL Postulate
8:22
Hypotenuse-Leg Postulate
8:23
Extra Example 1: LA Theorem & HL Postulate
10:57
Extra Example 2: Find x So That Each Pair of Triangles is Congruent
14:15
Extra Example 3: Two-column Proof
17:02
Extra Example 4: Two-column Proof
21:01
Indirect Proofs and Inequalities

33m 30s

Intro
0:00
Writing an Indirect Proof
0:09
Step 1
0:49
Step 2
2:32
Step 3
3:00
Indirect Proof
4:30
Example: 2 + 6 = 8
5:00
Example: The Suspect is Guilty
5:40
Example: Measure of Angle A < Measure of Angle B
6:06
Definition of Inequality
7:47
Definition of Inequality & Example
7:48
Properties of Inequality
9:55
Comparison Property
9:58
Transitive Property
10:33
Addition and Subtraction Properties
12:01
Multiplication and Division Properties
13:07
Exterior Angle Inequality Theorem
14:12
Example: Exterior Angle Inequality Theorem
14:13
Extra Example 1: Draw a Diagram for the Statement
18:32
Extra Example 2: Name the Property for Each Statement
19:56
Extra Example 3: State the Assumption
21:22
Extra Example 4: Write an Indirect Proof
25:39
Inequalities for Sides and Angles of a Triangle

17m 26s

Intro
0:00
Side to Angles
0:10
If One Side of a Triangle is Longer Than Another Side
0:11
Converse: Angles to Sides
1:57
If One Angle of a Triangle Has a Greater Measure Than Another Angle
1:58
Extra Example 1: Name the Angles in the Triangle From Least to Greatest
2:38
Extra Example 2: Find the Longest and Shortest Segment in the Triangle
3:47
Extra Example 3: Angles and Sides of a Triangle
4:51
Extra Example 4: Two-column Proof
9:08
Triangle Inequality

28m 11s

Intro
0:00
Triangle Inequality Theorem
0:05
Triangle Inequality Theorem
0:06
Triangle Inequality Theorem
4:22
Example 1: Triangle Inequality Theorem
4:23
Example 2: Triangle Inequality Theorem
9:40
Extra Example 1: Determine if the Three Numbers can Represent the Sides of a Triangle
12:00
Extra Example 2: Finding the Third Side of a Triangle
13:34
Extra Example 3: Always True, Sometimes True, or Never True
18:18
Extra Example 4: Triangle and Vertices
22:36
Inequalities Involving Two Triangles

29m 36s

Intro
0:00
SAS Inequality Theorem
0:06
SAS Inequality Theorem & Example
0:25
SSS Inequality Theorem
4:33
SSS Inequality Theorem & Example
4:34
Extra Example 1: Write an Inequality Comparing the Segments
6:08
Extra Example 2: Determine if the Statement is True
9:52
Extra Example 3: Write an Inequality for x
14:20
Extra Example 4: Two-column Proof
17:44
Section 6: Quadrilaterals
Parallelograms

29m 11s

Intro
0:00
Quadrilaterals
0:06
Four-sided Polygons
0:08
Non Examples of Quadrilaterals
0:47
Parallelograms
1:35
Parallelograms
1:36
Properties of Parallelograms
4:28
Opposite Sides of a Parallelogram are Congruent
4:29
Opposite Angles of a Parallelogram are Congruent
5:49
Angles and Diagonals
6:24
Consecutive Angles in a Parallelogram are Supplementary
6:25
The Diagonals of a Parallelogram Bisect Each Other
8:42
Extra Example 1: Complete Each Statement About the Parallelogram
10:26
Extra Example 2: Find the Values of x, y, and z of the Parallelogram
13:21
Extra Example 3: Find the Distance of Each Side to Verify the Parallelogram
16:35
Extra Example 4: Slope of Parallelogram
23:15
Proving Parallelograms

42m 43s

Intro
0:00
Parallelogram Theorems
0:09
Theorem 1
0:20
Theorem 2
1:50
Parallelogram Theorems, Cont.
3:10
Theorem 3
3:11
Theorem 4
4:15
Proving Parallelogram
6:21
Example: Determine if Quadrilateral ABCD is a Parallelogram
6:22
Summary
14:01
Both Pairs of Opposite Sides are Parallel
14:14
Both Pairs of Opposite Sides are Congruent
15:09
Both Pairs of Opposite Angles are Congruent
15:24
Diagonals Bisect Each Other
15:44
A Pair of Opposite Sides is Both Parallel and Congruent
16:13
Extra Example 1: Determine if Each Quadrilateral is a Parallelogram
16:54
Extra Example 2: Find the Value of x and y
20:23
Extra Example 3: Determine if the Quadrilateral ABCD is a Parallelogram
24:05
Extra Example 4: Two-column Proof
30:28
Rectangles

29m 47s

Intro
0:00
Rectangles
0:03
Definition of Rectangles
0:04
Diagonals of Rectangles
2:52
Rectangles: Diagonals Property 1
2:53
Rectangles: Diagonals Property 2
3:30
Proving a Rectangle
4:40
Example: Determine Whether Parallelogram ABCD is a Rectangle
4:41
Rectangles Summary
9:22
Opposite Sides are Congruent and Parallel
9:40
Opposite Angles are Congruent
9:51
Consecutive Angles are Supplementary
9:58
Diagonals are Congruent and Bisect Each Other
10:05
All Four Angles are Right Angles
10:40
Extra Example 1: Find the Value of x
11:03
Extra Example 2: Name All Congruent Sides and Angles
13:52
Extra Example 3: Always, Sometimes, or Never True
19:39
Extra Example 4: Determine if ABCD is a Rectangle
26:45
Squares and Rhombi

39m 14s

Intro
0:00
Rhombus
0:09
Definition of a Rhombus
0:10
Diagonals of a Rhombus
2:03
Rhombus: Diagonals Property 1
2:21
Rhombus: Diagonals Property 2
3:49
Rhombus: Diagonals Property 3
4:36
Rhombus
6:17
Example: Use the Rhombus to Find the Missing Value
6:18
Square
8:17
Definition of a Square
8:20
Summary Chart
11:06
Parallelogram
11:07
Rectangle
12:56
Rhombus
13:54
Square
14:44
Extra Example 1: Diagonal Property
15:44
Extra Example 2: Use Rhombus ABCD to Find the Missing Value
19:39
Extra Example 3: Always, Sometimes, or Never True
23:06
Extra Example 4: Determine the Quadrilateral
28:02
Trapezoids and Kites

30m 48s

Intro
0:00
Trapezoid
0:10
Definition of Trapezoid
0:12
Isosceles Trapezoid
2:57
Base Angles of an Isosceles Trapezoid
2:58
Diagonals of an Isosceles Trapezoid
4:05
Median of a Trapezoid
4:26
Median of a Trapezoid
4:27
Median of a Trapezoid
6:41
Median Formula
7:00
Kite
8:28
Definition of a Kite
8:29
Quadrilaterals Summary
11:19
A Quadrilateral with Two Pairs of Adjacent Congruent Sides
11:20
Extra Example 1: Isosceles Trapezoid
14:50
Extra Example 2: Median of Trapezoid
18:28
Extra Example 3: Always, Sometimes, or Never
24:13
Extra Example 4: Determine if the Figure is a Trapezoid
26:49
Section 7: Proportions and Similarity
Using Proportions and Ratios

20m 10s

Intro
0:00
Ratio
0:05
Definition and Examples of Writing Ratio
0:06
Proportion
2:05
Definition of Proportion
2:06
Examples of Proportion
2:29
Using Ratio
5:53
Example: Ratio
5:54
Extra Example 1: Find Three Ratios Equivalent to 2/5
9:28
Extra Example 2: Proportion and Cross Products
10:32
Extra Example 3: Express Each Ratio as a Fraction
13:18
Extra Example 4: Fin the Measure of a 3:4:5 Triangle
17:26
Similar Polygons

27m 53s

Intro
0:00
Similar Polygons
0:05
Definition of Similar Polygons
0:06
Example of Similar Polygons
2:32
Scale Factor
4:26
Scale Factor: Definition and Example
4:27
Extra Example 1: Determine if Each Pair of Figures is Similar
7:03
Extra Example 2: Find the Values of x and y
11:33
Extra Example 3: Similar Triangles
19:57
Extra Example 4: Draw Two Similar Figures
23:36
Similar Triangles

34m 10s

Intro
0:00
AA Similarity
0:10
Definition of AA Similarity
0:20
Example of AA Similarity
2:32
SSS Similarity
4:46
Definition of SSS Similarity
4:47
Example of SSS Similarity
6:00
SAS Similarity
8:04
Definition of SAS Similarity
8:05
Example of SAS Similarity
9:12
Extra Example 1: Determine Whether Each Pair of Triangles is Similar
10:59
Extra Example 2: Determine Which Triangles are Similar
16:08
Extra Example 3: Determine if the Statement is True or False
23:11
Extra Example 4: Write Two-Column Proof
26:25
Parallel Lines and Proportional Parts

24m 7s

Intro
0:00
Triangle Proportionality
0:07
Definition of Triangle Proportionality
0:08
Example of Triangle Proportionality
0:51
Triangle Proportionality Converse
2:19
Triangle Proportionality Converse
2:20
Triangle Mid-segment
3:42
Triangle Mid-segment: Definition and Example
3:43
Parallel Lines and Transversal
6:51
Parallel Lines and Transversal
6:52
Extra Example 1: Complete Each Statement
8:59
Extra Example 2: Determine if the Statement is True or False
12:28
Extra Example 3: Find the Value of x and y
15:35
Extra Example 4: Find Midpoints of a Triangle
20:43
Parts of Similar Triangles

27m 6s

Intro
0:00
Proportional Perimeters
0:09
Proportional Perimeters: Definition and Example
0:10
Similar Altitudes
2:23
Similar Altitudes: Definition and Example
2:24
Similar Angle Bisectors
4:50
Similar Angle Bisectors: Definition and Example
4:51
Similar Medians
6:05
Similar Medians: Definition and Example
6:06
Angle Bisector Theorem
7:33
Angle Bisector Theorem
7:34
Extra Example 1: Parts of Similar Triangles
10:52
Extra Example 2: Parts of Similar Triangles
14:57
Extra Example 3: Parts of Similar Triangles
19:27
Extra Example 4: Find the Perimeter of Triangle ABC
23:14
Section 8: Applying Right Triangles & Trigonometry
Pythagorean Theorem

21m 14s

Intro
0:00
Pythagorean Theorem
0:05
Pythagorean Theorem & Example
0:06
Pythagorean Converse
1:20
Pythagorean Converse & Example
1:21
Pythagorean Triple
2:42
Pythagorean Triple
2:43
Extra Example 1: Find the Missing Side
4:59
Extra Example 2: Determine Right Triangle
7:40
Extra Example 3: Determine Pythagorean Triple
11:30
Extra Example 4: Vertices and Right Triangle
14:29
Geometric Mean

40m 59s

Intro
0:00
Geometric Mean
0:04
Geometric Mean & Example
0:05
Similar Triangles
4:32
Similar Triangles
4:33
Geometric Mean-Altitude
11:10
Geometric Mean-Altitude & Example
11:11
Geometric Mean-Leg
14:47
Geometric Mean-Leg & Example
14:18
Extra Example 1: Geometric Mean Between Each Pair of Numbers
20:10
Extra Example 2: Similar Triangles
23:46
Extra Example 3: Geometric Mean of Triangles
28:30
Extra Example 4: Geometric Mean of Triangles
36:58
Special Right Triangles

37m 57s

Intro
0:00
45-45-90 Triangles
0:06
Definition of 45-45-90 Triangles
0:25
45-45-90 Triangles
5:51
Example: Find n
5:52
30-60-90 Triangles
8:59
Definition of 30-60-90 Triangles
9:00
30-60-90 Triangles
12:25
Example: Find n
12:26
Extra Example 1: Special Right Triangles
15:08
Extra Example 2: Special Right Triangles
18:22
Extra Example 3: Word Problems & Special Triangles
27:40
Extra Example 4: Hexagon & Special Triangles
33:51
Ratios in Right Triangles

40m 37s

Intro
0:00
Trigonometric Ratios
0:08
Definition of Trigonometry
0:13
Sine (sin), Cosine (cos), & Tangent (tan)
0:50
Trigonometric Ratios
3:04
Trig Functions
3:05
Inverse Trig Functions
5:02
SOHCAHTOA
8:16
sin x
9:07
cos x
10:00
tan x
10:32
Example: SOHCAHTOA & Triangle
12:10
Extra Example 1: Find the Value of Each Ratio or Angle Measure
14:36
Extra Example 2: Find Sin, Cos, and Tan
18:51
Extra Example 3: Find the Value of x Using SOHCAHTOA
22:55
Extra Example 4: Trigonometric Ratios in Right Triangles
32:13
Angles of Elevation and Depression

21m 4s

Intro
0:00
Angle of Elevation
0:10
Definition of Angle of Elevation & Example
0:11
Angle of Depression
1:19
Definition of Angle of Depression & Example
1:20
Extra Example 1: Name the Angle of Elevation and Depression
2:22
Extra Example 2: Word Problem & Angle of Depression
4:41
Extra Example 3: Word Problem & Angle of Elevation
14:02
Extra Example 4: Find the Missing Measure
18:10
Law of Sines

35m 25s

Intro
0:00
Law of Sines
0:20
Law of Sines
0:21
Law of Sines
3:34
Example: Find b
3:35
Solving the Triangle
9:19
Example: Using the Law of Sines to Solve Triangle
9:20
Extra Example 1: Law of Sines and Triangle
17:43
Extra Example 2: Law of Sines and Triangle
20:06
Extra Example 3: Law of Sines and Triangle
23:54
Extra Example 4: Law of Sines and Triangle
28:59
Law of Cosines

52m 43s

Intro
0:00
Law of Cosines
0:35
Law of Cosines
0:36
Law of Cosines
6:22
Use the Law of Cosines When Both are True
6:23
Law of Cosines
8:35
Example: Law of Cosines
8:36
Extra Example 1: Law of Sines or Law of Cosines?
13:35
Extra Example 2: Use the Law of Cosines to Find the Missing Measure
17:02
Extra Example 3: Solve the Triangle
30:49
Extra Example 4: Find the Measure of Each Diagonal of the Parallelogram
41:39
Section 9: Circles
Segments in a Circle

22m 43s

Intro
0:00
Segments in a Circle
0:10
Circle
0:11
Chord
0:59
Diameter
1:32
Radius
2:07
Secant
2:17
Tangent
3:10
Circumference
3:56
Introduction to Circumference
3:57
Example: Find the Circumference of the Circle
5:09
Circumference
6:40
Example: Find the Circumference of the Circle
6:41
Extra Example 1: Use the Circle to Answer the Following
9:10
Extra Example 2: Find the Missing Measure
12:53
Extra Example 3: Given the Circumference, Find the Perimeter of the Triangle
15:51
Extra Example 4: Find the Circumference of Each Circle
19:24
Angles and Arc

35m 24s

Intro
0:00
Central Angle
0:06
Definition of Central Angle
0:07
Sum of Central Angles
1:17
Sum of Central Angles
1:18
Arcs
2:27
Minor Arc
2:30
Major Arc
3:47
Arc Measure
5:24
Measure of Minor Arc
5:24
Measure of Major Arc
6:53
Measure of a Semicircle
7:11
Arc Addition Postulate
8:25
Arc Addition Postulate
8:26
Arc Length
9:43
Arc Length and Example
9:44
Concentric Circles
16:05
Concentric Circles
16:06
Congruent Circles and Arcs
17:50
Congruent Circles
17:51
Congruent Arcs
18:47
Extra Example 1: Minor Arc, Major Arc, and Semicircle
20:14
Extra Example 2: Measure and Length of Arc
22:52
Extra Example 3: Congruent Arcs
25:48
Extra Example 4: Angles and Arcs
30:33
Arcs and Chords

21m 51s

Intro
0:00
Arcs and Chords
0:07
Arc of the Chord
0:08
Theorem 1: Congruent Minor Arcs
1:01
Inscribed Polygon
2:10
Inscribed Polygon
2:11
Arcs and Chords
3:18
Theorem 2: When a Diameter is Perpendicular to a Chord
3:19
Arcs and Chords
5:05
Theorem 3: Congruent Chords
5:06
Extra Example 1: Congruent Arcs
10:35
Extra Example 2: Length of Arc
13:50
Extra Example 3: Arcs and Chords
17:09
Extra Example 4: Arcs and Chords
19:45
Inscribed Angles

27m 53s

Intro
0:00
Inscribed Angles
0:07
Definition of Inscribed Angles
0:08
Inscribed Angles
0:58
Inscribed Angle Theorem 1
0:59
Inscribed Angles
3:29
Inscribed Angle Theorem 2
3:30
Inscribed Angles
4:38
Inscribed Angle Theorem 3
4:39
Inscribed Quadrilateral
5:50
Inscribed Quadrilateral
5:51
Extra Example 1: Central Angle, Inscribed Angle, and Intercepted Arc
7:02
Extra Example 2: Inscribed Angles
9:24
Extra Example 3: Inscribed Angles
14:00
Extra Example 4: Complete the Proof
17:58
Tangents

26m 16s

Intro
0:00
Tangent Theorems
0:04
Tangent Theorem 1
0:05
Tangent Theorem 1 Converse
0:55
Common Tangents
1:34
Common External Tangent
2:12
Common Internal Tangent
2:30
Tangent Segments
3:08
Tangent Segments
3:09
Circumscribed Polygons
4:11
Circumscribed Polygons
4:12
Extra Example 1: Tangents & Circumscribed Polygons
5:50
Extra Example 2: Tangents & Circumscribed Polygons
8:35
Extra Example 3: Tangents & Circumscribed Polygons
11:50
Extra Example 4: Tangents & Circumscribed Polygons
15:43
Secants, Tangents, & Angle Measures

27m 50s

Intro
0:00
Secant
0:08
Secant
0:09
Secant and Tangent
0:49
Secant and Tangent
0:50
Interior Angles
2:56
Secants & Interior Angles
2:57
Exterior Angles
7:21
Secants & Exterior Angles
7:22
Extra Example 1: Secants, Tangents, & Angle Measures
10:53
Extra Example 2: Secants, Tangents, & Angle Measures
13:31
Extra Example 3: Secants, Tangents, & Angle Measures
19:54
Extra Example 4: Secants, Tangents, & Angle Measures
22:29
Special Segments in a Circle

23m 8s

Intro
0:00
Chord Segments
0:05
Chord Segments
0:06
Secant Segments
1:36
Secant Segments
1:37
Tangent and Secant Segments
4:10
Tangent and Secant Segments
4:11
Extra Example 1: Special Segments in a Circle
5:53
Extra Example 2: Special Segments in a Circle
7:58
Extra Example 3: Special Segments in a Circle
11:24
Extra Example 4: Special Segments in a Circle
18:09
Equations of Circles

27m 1s

Intro
0:00
Equation of a Circle
0:06
Standard Equation of a Circle
0:07
Example 1: Equation of a Circle
0:57
Example 2: Equation of a Circle
1:36
Extra Example 1: Determine the Coordinates of the Center and the Radius
4:56
Extra Example 2: Write an Equation Based on the Given Information
7:53
Extra Example 3: Graph Each Circle
16:48
Extra Example 4: Write the Equation of Each Circle
19:17
Section 10: Polygons & Area
Polygons

27m 24s

Intro
0:00
Polygons
0:10
Polygon vs. Not Polygon
0:18
Convex and Concave
1:46
Convex vs. Concave Polygon
1:52
Regular Polygon
4:04
Regular Polygon
4:05
Interior Angle Sum Theorem
4:53
Triangle
5:03
Quadrilateral
6:05
Pentagon
6:38
Hexagon
7:59
20-Gon
9:36
Exterior Angle Sum Theorem
12:04
Exterior Angle Sum Theorem
12:05
Extra Example 1: Drawing Polygons
13:51
Extra Example 2: Convex Polygon
15:16
Extra Example 3: Exterior Angle Sum Theorem
18:21
Extra Example 4: Interior Angle Sum Theorem
22:20
Area of Parallelograms

17m 46s

Intro
0:00
Parallelograms
0:06
Definition and Area Formula
0:07
Area of Figure
2:00
Area of Figure
2:01
Extra Example 1:Find the Area of the Shaded Area
3:14
Extra Example 2: Find the Height and Area of the Parallelogram
6:00
Extra Example 3: Find the Area of the Parallelogram Given Coordinates and Vertices
10:11
Extra Example 4: Find the Area of the Figure
14:31
Area of Triangles Rhombi, & Trapezoids

20m 31s

Intro
0:00
Area of a Triangle
0:06
Area of a Triangle: Formula and Example
0:07
Area of a Trapezoid
2:31
Area of a Trapezoid: Formula
2:32
Area of a Trapezoid: Example
6:55
Area of a Rhombus
8:05
Area of a Rhombus: Formula and Example
8:06
Extra Example 1: Find the Area of the Polygon
9:51
Extra Example 2: Find the Area of the Figure
11:19
Extra Example 3: Find the Area of the Figure
14:16
Extra Example 4: Find the Height of the Trapezoid
18:10
Area of Regular Polygons & Circles

36m 43s

Intro
0:00
Regular Polygon
0:08
SOHCAHTOA
0:54
30-60-90 Triangle
1:52
45-45-90 Triangle
2:40
Area of a Regular Polygon
3:39
Area of a Regular Polygon
3:40
Are of a Circle
7:55
Are of a Circle
7:56
Extra Example 1: Find the Area of the Regular Polygon
8:22
Extra Example 2: Find the Area of the Regular Polygon
16:48
Extra Example 3: Find the Area of the Shaded Region
24:11
Extra Example 4: Find the Area of the Shaded Region
32:24
Perimeter & Area of Similar Figures

18m 17s

Intro
0:00
Perimeter of Similar Figures
0:08
Example: Scale Factor & Perimeter of Similar Figures
0:09
Area of Similar Figures
2:44
Example:Scale Factor & Area of Similar Figures
2:55
Extra Example 1: Complete the Table
6:09
Extra Example 2: Find the Ratios of the Perimeter and Area of the Similar Figures
8:56
Extra Example 3: Find the Unknown Area
12:04
Extra Example 4: Use the Given Area to Find AB
14:26
Geometric Probability

38m 40s

Intro
0:00
Length Probability Postulate
0:05
Length Probability Postulate
0:06
Are Probability Postulate
2:34
Are Probability Postulate
2:35
Are of a Sector of a Circle
4:11
Are of a Sector of a Circle Formula
4:12
Are of a Sector of a Circle Example
7:51
Extra Example 1: Length Probability
11:07
Extra Example 2: Area Probability
12:14
Extra Example 3: Area Probability
17:17
Extra Example 4: Area of a Sector of a Circle
26:23
Section 11: Solids
Three-Dimensional Figures

23m 39s

Intro
0:00
Polyhedrons
0:05
Polyhedrons: Definition and Examples
0:06
Faces
1:08
Edges
1:55
Vertices
2:23
Solids
2:51
Pyramid
2:54
Cylinder
3:45
Cone
4:09
Sphere
4:23
Prisms
5:00
Rectangular, Regular, and Cube Prisms
5:02
Platonic Solids
9:48
Five Types of Regular Polyhedra
9:49
Slices and Cross Sections
12:07
Slices
12:08
Cross Sections
12:47
Extra Example 1: Name the Edges, Faces, and Vertices of the Polyhedron
14:23
Extra Example 2: Determine if the Figure is a Polyhedron and Explain Why
17:37
Extra Example 3: Describe the Slice Resulting from the Cut
19:12
Extra Example 4: Describe the Shape of the Intersection
21:25
Surface Area of Prisms and Cylinders

38m 50s

Intro
0:00
Prisms
0:06
Bases
0:07
Lateral Faces
0:52
Lateral Edges
1:19
Altitude
1:58
Prisms
2:24
Right Prism
2:25
Oblique Prism
2:56
Classifying Prisms
3:27
Right Rectangular Prism
3:28
4:55
Oblique Pentagonal Prism
6:26
Right Hexagonal Prism
7:14
Lateral Area of a Prism
7:42
Lateral Area of a Prism
7:43
Surface Area of a Prism
13:44
Surface Area of a Prism
13:45
Cylinder
16:18
Cylinder: Right and Oblique
16:19
Lateral Area of a Cylinder
18:02
Lateral Area of a Cylinder
18:03
Surface Area of a Cylinder
20:54
Surface Area of a Cylinder
20:55
Extra Example 1: Find the Lateral Area and Surface Are of the Prism
21:51
Extra Example 2: Find the Lateral Area of the Prism
28:15
Extra Example 3: Find the Surface Area of the Prism
31:57
Extra Example 4: Find the Lateral Area and Surface Area of the Cylinder
34:17
Surface Area of Pyramids and Cones

26m 10s

Intro
0:00
Pyramids
0:07
Pyramids
0:08
Regular Pyramids
1:52
Regular Pyramids
1:53
Lateral Area of a Pyramid
4:33
Lateral Area of a Pyramid
4:34
Surface Area of a Pyramid
9:19
Surface Area of a Pyramid
9:20
Cone
10:09
Right and Oblique Cone
10:10
Lateral Area and Surface Area of a Right Cone
11:20
Lateral Area and Surface Are of a Right Cone
11:21
Extra Example 1: Pyramid and Prism
13:11
Extra Example 2: Find the Lateral Area of the Regular Pyramid
15:00
Extra Example 3: Find the Surface Area of the Pyramid
18:29
Extra Example 4: Find the Lateral Area and Surface Area of the Cone
22:08
Volume of Prisms and Cylinders

21m 59s

Intro
0:00
Volume of Prism
0:08
Volume of Prism
0:10
Volume of Cylinder
3:38
Volume of Cylinder
3:39
Extra Example 1: Find the Volume of the Prism
5:10
Extra Example 2: Find the Volume of the Cylinder
8:03
Extra Example 3: Find the Volume of the Prism
9:35
Extra Example 4: Find the Volume of the Solid
19:06
Volume of Pyramids and Cones

22m 2s

Intro
0:00
Volume of a Cone
0:08
Volume of a Cone: Example
0:10
Volume of a Pyramid
3:02
Volume of a Pyramid: Example
3:03
Extra Example 1: Find the Volume of the Pyramid
4:56
Extra Example 2: Find the Volume of the Solid
6:01
Extra Example 3: Find the Volume of the Pyramid
10:28
Extra Example 4: Find the Volume of the Octahedron
16:23
Surface Area and Volume of Spheres

14m 46s

Intro
0:00
Special Segments
0:06
Radius
0:07
Chord
0:31
Diameter
0:55
Tangent
1:20
Sphere
1:43
Plane & Sphere
1:44
Hemisphere
2:56
Surface Area of a Sphere
3:25
Surface Area of a Sphere
3:26
Volume of a Sphere
4:08
Volume of a Sphere
4:09
Extra Example 1: Determine Whether Each Statement is True or False
4:24
Extra Example 2: Find the Surface Area of the Sphere
6:17
Extra Example 3: Find the Volume of the Sphere with a Diameter of 20 Meters
7:25
Extra Example 4: Find the Surface Area and Volume of the Solid
9:17
Congruent and Similar Solids

16m 6s

Intro
0:00
Scale Factor
0:06
Scale Factor: Definition and Example
0:08
Congruent Solids
1:09
Congruent Solids
1:10
Similar Solids
2:17
Similar Solids
2:18
Extra Example 1: Determine if Each Pair of Solids is Similar, Congruent, or Neither
3:35
Extra Example 2: Determine if Each Statement is True or False
7:47
Extra Example 3: Find the Scale Factor and the Ratio of the Surface Areas and Volume
10:14
Extra Example 4: Find the Volume of the Larger Prism
12:14
Section 12: Transformational Geometry
Mapping

14m 12s

Intro
0:00
Transformation
0:04
Rotation
0:32
Translation
1:03
Reflection
1:17
Dilation
1:24
Transformations
1:45
Examples
1:46
Congruence Transformation
2:51
Congruence Transformation
2:52
Extra Example 1: Describe the Transformation that Occurred in the Mappings
3:37
Extra Example 2: Determine if the Transformation is an Isometry
5:16
Extra Example 3: Isometry
8:16
Reflections

23m 17s

Intro
0:00
Reflection
0:05
Definition of Reflection
0:06
Line of Reflection
0:35
Point of Reflection
1:22
Symmetry
1:59
Line of Symmetry
2:00
Point of Symmetry
2:48
Extra Example 1: Draw the Image over the Line of Reflection and the Point of Reflection
3:45
Extra Example 2: Determine Lines and Point of Symmetry
6:59
Extra Example 3: Graph the Reflection of the Polygon
11:15
Extra Example 4: Graph the Coordinates
16:07
Translations

18m 43s

Intro
0:00
Translation
0:05
Translation: Preimage & Image
0:06
Example
0:56
Composite of Reflections
6:28
Composite of Reflections
6:29
Extra Example 1: Translation
7:48
Extra Example 2: Image, Preimage, and Translation
12:38
Extra Example 3: Find the Translation Image Using a Composite of Reflections
15:08
Extra Example 4: Find the Value of Each Variable in the Translation
17:18
Rotations

21m 26s

Intro
0:00
Rotations
0:04
Rotations
0:05
Performing Rotations
2:13
Composite of Two Successive Reflections over Two Intersecting Lines
2:14
Angle of Rotation: Angle Formed by Intersecting Lines
4:29
Angle of Rotation
5:30
Rotation Postulate
5:31
Extra Example 1: Find the Rotated Image
7:32
Extra Example 2: Rotations and Coordinate Plane
10:33
Extra Example 3: Find the Value of Each Variable in the Rotation
14:29
Extra Example 4: Draw the Polygon Rotated 90 Degree Clockwise about P
16:13
Dilation

37m 6s

Intro
0:00
Dilations
0:06
Dilations
0:07
Scale Factor
1:36
Scale Factor
1:37
Example 1
2:06
Example 2
6:22
Scale Factor
8:20
Positive Scale Factor
8:21
Negative Scale Factor
9:25
Enlargement
12:43
Reduction
13:52
Extra Example 1: Find the Scale Factor
16:39
Extra Example 2: Find the Measure of the Dilation Image
19:32
Extra Example 3: Find the Coordinates of the Image with Scale Factor and the Origin as the Center of Dilation
26:18
Extra Example 4: Graphing Polygon, Dilation, and Scale Factor
32:08
Loading...
This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Geometry
Bookmark & Share Embed

Share this knowledge with your friends!

Copy & Paste this embed code into your website’s HTML

Please ensure that your website editor is in text mode when you paste the code.
(In Wordpress, the mode button is on the top right corner.)
  ×
  • - Allow users to view the embedded video in full-size.
Since this lesson is not free, only the preview will appear on your website.

  • Discussion

  • Answer Engine

  • Study Guides

  • Practice Questions

  • Download Lecture Slides

  • Table of Contents

  • Transcription

  • Related Books

Lecture Comments (4)

0 answers

Post by Jamal Salim on October 27, 2015

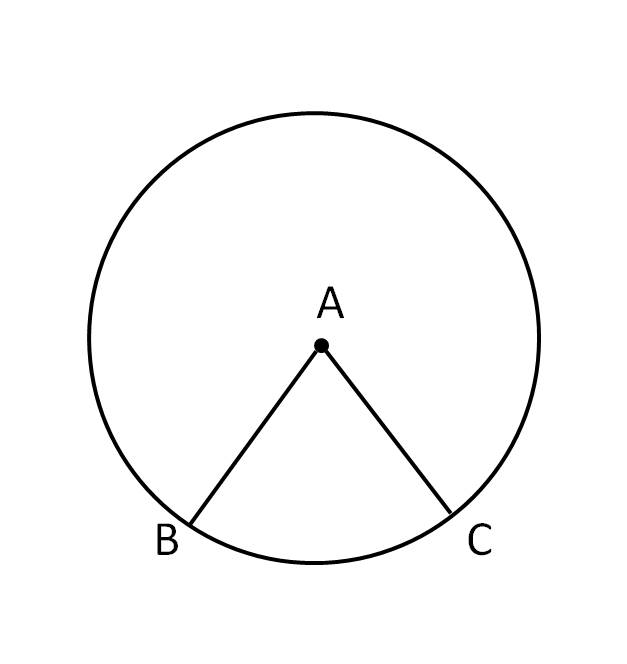
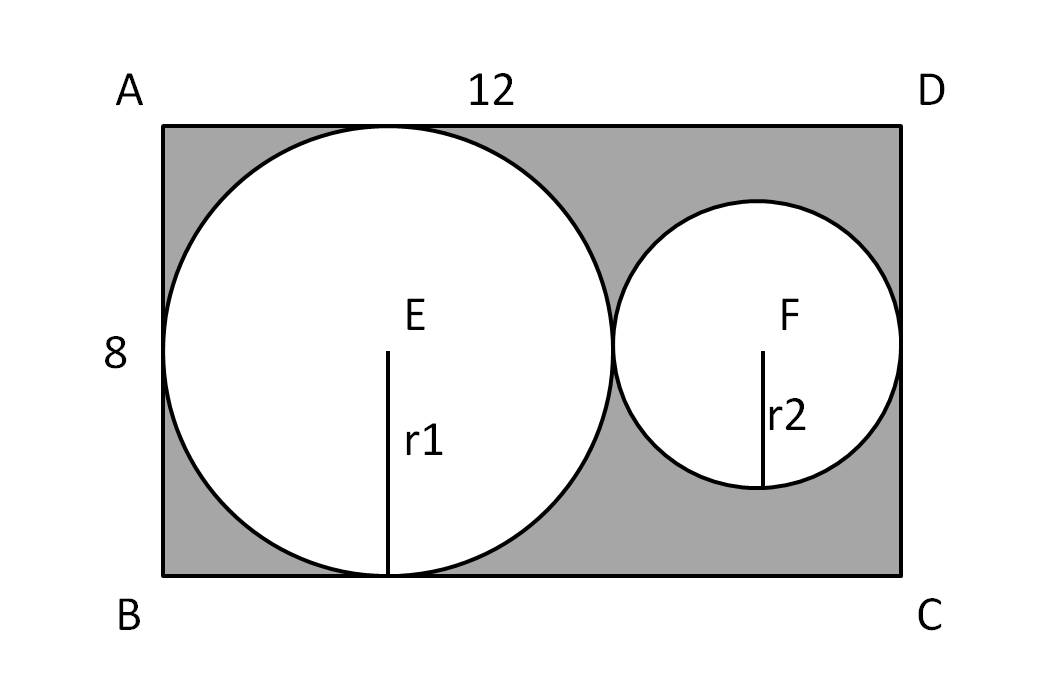
in Example 2 you can find the probability direct using 72/360 = 1/5 because (Pi)r2 will cancel each other

2 answers

Last reply by: Jamal Salim
Tue Oct 27, 2015 8:57 PM

Post by Mirza Baig on December 6, 2013

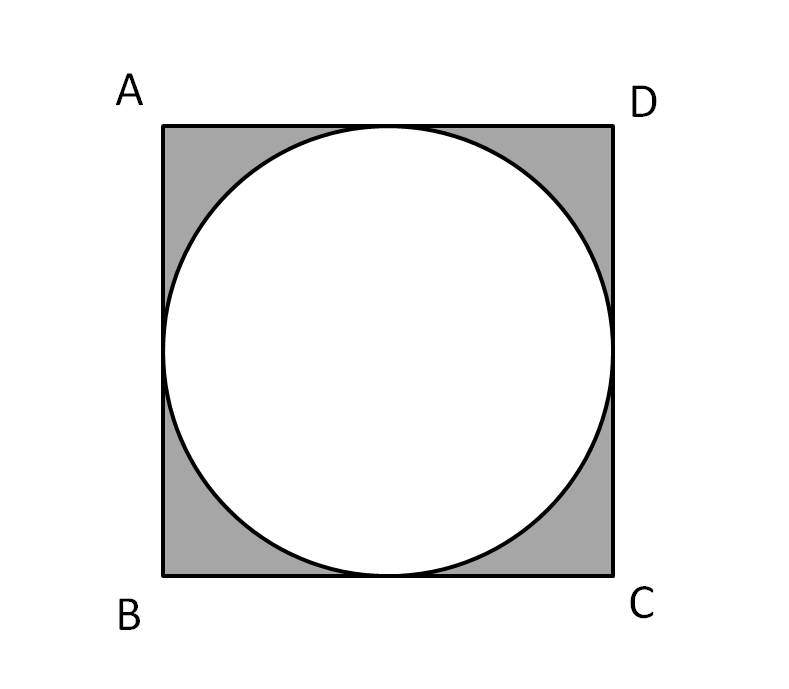
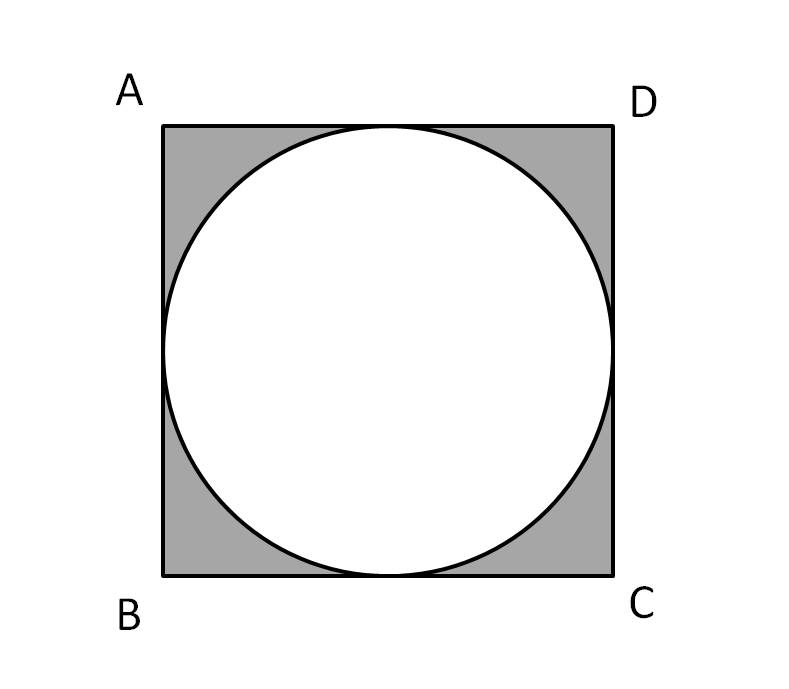
I think the example 3 where you find the side of a square and you said that it was 10 radical 2 but in my opinion i think that's wrong because we know that  squares sides and hypotenuse are same because  of Pythagorean theorem
and so add 10+10 = 20,20 is the side of a square so the area of a square would be 400cm^2.

Geometric Probability

  • Length Probability Postulate: If a point on AB is chosen at random and C is between A and B, then the probability that the point is on AC is AC/AB
  • Area Probability Postulate: If a point in region A is chosen at random, then the probability that the point is in region B, which is the interior of region A, is the area of B to the area of A
  • Area of a Sector of a Circle: A sector of a circle is a region of a circle bounded by a central angle and its intercepted arc. Area = (central angle)/(360 degrees) × πr2

Geometric Probability


Find the probability that a point is on ―AB .
[AB/AC] = [6/(6 + 10)] = [3/8]

―AB = ―AC , if a point is in ∆ABC,find the probability that it is in ∆ABD.
  • ∆ABD ≅∆ACD
  • [Area of ∆ ABD/Area of ∆ ACD] = [1/2]
The probability is [1/2]

Determine whether the following statement is true or false.
If a point is in circle A, then it is also in pentagon BCDEF.
False

Circle A, m∠BAC = 60o, AB = 5, find the area of sector ABC.
  • Area = [(m∠BAC)/360]*πr2
  • Area = [60/360]*3.14*52
Area = 94.2

Rhombus ABCD, if a point is in rhombus ABCD, find the probability that it is also in ∆ABE.
  • [Area of ∆ ABE/Area of rhombus ABCD] = [([1/2]*AE*BE)/([1/2]*AC*BD)] = [AE*BE/AC*BD] = [AE*BE/(2AE)*(2BE)] = [1/4]
The probability is [1/4]

Trapezoid ABCD,―BE ⊥―AD , if a point is in trapezoid ABCD, find the probability that it is in ∆ABE.
  • [Area of ∆ ABE/Area of trapezoid ABCD] = [([1/2]*AE*BE)/([1/2]*(AD + BC)*BE)] = [AE/(AD + BC)] = [2/((2 + 10) + 7)] = [2/19]
[2/19]

Square ABCD, find the probability that a point is in the square but outside the circle.
  • [Area of the circle/Area of the square] = [(πr2)/((2r)2)] = [(π)/4] = [3.14/4] = 0.785
  • The probability that the point is in the shaded region = 1 − 0.785 = 0.215
0.215

Rectangle ABCD, circle E and circle F, a point is in the rectangle, find the probability that it is in the shaded region.
  • r1 = [1/2]AB = 4
  • 2r1 + 2r2 = BC
  • r2 = [1/2]BC − r1 = [1/2]*12 − 4 = 2
  • Area of circle E = πr12 = 3.14*4*4 = 50.24
  • Area of circle F = πr22 = 3.14*2*2 = 12.56
  • Area of rectangle ABCD = 8*12 = 96
  • Area of shaded region = 96 − 50.25 − 12.56 = 33.2
  • The probability that the point is in the shaded region: [33.2/96] = 0.346
0.346

Determine whether the following statement is true or false.
If a point is in the circle, then it is also in square ABCD.
True
Determine whether the following statement is true or false.
For two parallel lines, if a point is on one line, then the probability that the point is also on the other line is 0.
True

*These practice questions are only helpful when you work on them offline on a piece of paper and then use the solution steps function to check your answer.

Answer

Geometric Probability

Lecture Slides are screen-captured images of important points in the lecture. Students can download and print out these lecture slide images to do practice problems as well as take notes while watching the lecture.

  • Intro 0:00
  • Length Probability Postulate 0:05
    • Length Probability Postulate
  • Are Probability Postulate 2:34
    • Are Probability Postulate
  • Are of a Sector of a Circle 4:11
    • Are of a Sector of a Circle Formula
    • Are of a Sector of a Circle Example
  • Extra Example 1: Length Probability 11:07
  • Extra Example 2: Area Probability 12:14
  • Extra Example 3: Area Probability 17:17
  • Extra Example 4: Area of a Sector of a Circle 26:23

Transcription: Geometric Probability

Welcome back to Educator.com.0000

For the next lesson, we are going to go over geometric probability.0001

The first thing that we are going to go over is the Length Probability Postulate.0008

It is when we are using segments for probability.0013

If a point on segment AB is chosen at random, and point C is between A and B, then the probability that the point is on AC0018

is going to be (and this is a ratio) segment AC, over AB.0033

Now, if you remember probability, probability measures the part over the whole.0041

You can also think of the top number as the desired outcome, over the total outcome, the total possible number of all of the different types of possible outcomes.0052

So then, it is a desired outcome, what you are looking for, over the total--over the whole thing.0077

So, it is just part over whole; this is the most basic way you can remember probability, part over whole.0083

Here, the same thing applies to the Length Probability Postulate; you are looking at the part.0091

You are looking at what the desired outcome is, which is the point being on AC, over the whole thing; that is AB--that is the whole thing.0099

It is AC to AB--always part over whole.0110

So, let's say that this right here is 5; CB is 5; the probability of a point landing on AC...what is AC?0116

That is the desired outcome; that is the top number, which is 5, over the whole thing (it is not 5; it is not the other half);0128

it is the whole thing, which is AB, and that is 10; so when I simplify this, this becomes 1/2.0139

The probability of landing on AC is 1/2.0148

And for the Area Probability Postulate, when you are talking about the probability of something to do with area, you are looking at space.0156

So, you are looking to see, for example, maybe a dart hitting the dartboard; that is area, because it is space that you are looking at.0166

If you look to see, maybe, a spinner (we are going to have both of those for our examples) landing on a certain space, that is area.0178

So, that has to do with this probability; and this postulate says that if a point in region A0191

(this rectangle is region A) is chosen at random, then the probability that the point is in region B0199

(which is inside region A) is going to be the area of region B, over...remember: the whole thing is the area of region A.0207

Region A is the whole thing; the area of the whole thing is the total,0231

and the top one will be the area of the desired outcome, or the part that we were just looking at; and that is region B.0238

The area of a sector of a circle: now, a sector is this little piece right here.0254

This is the center; the sector is the area of this piece, so it is bounded by the central angle0264

(this is a central angle right here; this angle is a central angle, so if I need the θ, that is the central angle) and its intercepted arc.0273

This is the intercepted arc; so those are the boundaries, this angle and that.0283

This whole thing is called a sector; now, I like to refer to the sector as a pizza slice.0289

Think of this whole thing as a pizza; this is a slice of pizza; so a sector is a slice of pizza.0300

We are finding the area of that slice; to find the area of this, it would be this formula:0309

the central angle (which is this angle right here, this central angle) over 360...0318

now, why is it over 360?--because going all the way around a full circle, including that, is 360; so it is like the part over the whole,0326

the central angle over the whole thing, which is 360...times the area of the circle.0337

Now, another way (an easier way, I think) would be (to figure out how to find the area of this):0346

instead of looking at this formula, I like to use proportions.0355

So, what we can do to find the area of this pizza slice right here: remember: a proportion is a ratio equaling another ratio;0359

so, we are going to look at the probability (probabilities are ratios, something to something, which is part to whole)0373

of the measures to the areas, because we are looking both: we are looking at measure, and we are looking at area.0387

So, for the measures, the part over the whole for the angle measures is going to be the central angle, over the whole thing, which is 360.0403

And the probability of the area...isn't that part over whole, also?...so the part will be the area of the sector.0422

That is the area of the sector; so let's just call that A for area of the sector...over the whole thing, which is0429

(the area of this whole circle is going to be) πr2.0440

Again, the ratio (or probability) of the part to the whole is the angle measure to the whole thing.0445

And the ratio of the areas is going to be the area of the sector, over the area of the circle, because this is part to whole.0459

We are going to make them equal to each other; that is our proportion; and you are just basically going to solve.0467

Let's say that this angle measure is 40, and the radius, r, is 6.0475

If this is 40, that is the part; that is 40 degrees, over...what is the whole thing?...360 degrees, is equal to the area of the sector;0497

that is what we are looking for; that is the area of the sector, over the area of the whole thing; that is the circle, so it is πr2.0512

So, that is π(6)2; and if you are going to solve this out, remember how you solve proportions.0524

You do cross-multiplying; so then, the area of the sector, times 360, times a, equals 40 degrees times π(6)2.0531

And when you solve this out, you divide this by 360, because we are solving for the a.0558

Now, if you look at this, this is exactly the same thing as this right here: the central angle,0568

the angle of that right there, divided by the 360, the whole circle, times the area of the circle--that is πr2.0579

It is the same exact thing; if you want to just use this, that is fine--it is the same exact thing.0591

But this way, you just know that you are looking at the part, the angle measure, over the whole, the circle's angle measure.0597

That is equal to the area of the sector (that is the part), over the area of the whole circle.0608

It is part over whole, for angle measures, equals part over whole, for the areas.0612

And that is just a way for you to be able to solve this out without having to memorize this formula.0620

And then, we solve this out; and you can just do that on your calculator; I have a calculator here on my screen.0627

I get that my area is 12.57; and again, that is the area of this sector, the pizza slice; and that is units of area, squared.0642

That is the area of a sector.0663

Let's go ahead and do some more examples: What is the probability that a point is on XY?0668

Again, for probability, we are looking at part to whole; so the desired outcome, the part that we are looking for, is XY;0675

that is going to be my numerator--that is the top part of my ratio--so XY is from 0 to 2; that is 2 units.0685

It is XY; again, we are looking at XY over the whole thing, which is XZ, so that is 2 over...the whole thing, from X to Z, is 10.0698

If I simplify this, this becomes 1/5, because 2 goes into both; it is a factor of both 2 and 10.0715

I can divide this by 2 and divide that by 2, and I get 1/5; that is the probability that a point will land on XY.0723

Find the probability of the spinner landing on orange, this space right here; here is that spinner.0736

This angle measure is 72, and the radius is 4; so, if this is 4, then we know that any segment from the center to the circle is going to be 4.0749

OK, so then, I want to use that proportion: the angle measure, over the measure of the circle, the total angle measure,0767

is equal to the area of the sector, over the whole thing (is going to be the area of the circle; and that just means "circle").0794

This is my proportion: the angle measure...any time I am dealing with the part (since it is always part over whole),0810

it is always going to be about the sector, this piece right here, the orange; and then, any time I am talking about the whole,0821

it is going to be the whole circle...(that is that) is 72 degrees, over the whole thing (is 360), is equal to0828

the area of the sector (and again, that is what I am looking for, so I can just say A for area of the sector),0842

over the area of the circle (that is the whole thing); and that is πr2.0850

My radius is 4, squared; so then, I can go ahead and cross-multiply.0859

360A = 72(π)(42); then, to solve for A, divide the 360; divide this whole thing by 360.0870

And then, from there, you can just use your calculator: 72 times π times the 42...and then divide 360; you get 10.05.0891

And we have inches here for units, so it is inches squared; that is the area of this orange.0919

Now, to find the probability...we found the area of this orange; and be careful, because,0926

if they ask you for the area of this base right here, then that would be our answer; but they are asking for a probability0933

of landing on orange; and any time you are looking at probability, you are always looking at part over whole.0939

And again, since we are talking about area, it is the area of the orange, over the area of the whole thing.0947

I found the area of a sector; now, to find the area of the whole thing, the area of the circle is πr2.0958

And all you have to do is...we know that r is 4, so 16 times π is 50.27 inches squared; that is the area of the circle.0970

And then, the probability is going to just be (I'll write it on this side) 10.05/50.27.0990

You can change this to a decimal, so you can go ahead and divide this; or maybe you can just leave it like that,1007

depending on how your teacher wants you to write the answer.1015

You can definitely have probability as a decimal; you can just go ahead and take this and divide it by this number; and that would be your answer.1020

This is the probability, part over whole, the area of the orange over the area of the circle.1028

The circle is circumscribed about a square; if a dart is thrown at the circle, what is the probability that it lands in the circle, but outside the square?1040

We want to know what the probability is of landing in the gray area: it said "in the circle, but outside the square"; that is all the gray area.1055

That is the probability: they are not asking for the area of that part; they are asking for the probability of landing on that part.1066

So then, we have to make sure that we are going to do the part over the whole.1073

First, I have to find the area of that gray area, because that is my desired outcome; that is my part.1082

The desired outcome is the area of the gray, over the whole thing, which would be the area of the circle, because that is the whole thing.1087

So then, my part is going to be, again, area of gray over the area of the circle.1097

To find the area of the gray region, we have to first find the area of the circle and subtract the area of the square.1117

The area of the gray is going to be the circle, minus the square.1132

The area of the circle is πr2, minus...the area of this is going to be side squared.1154

We know that the radius is 10, because, from the center of the circle to the point on the circle, it is π(10)2;1168

minus...do we know what the side is?...we actually don't, because this is from the center to the vertex of this square.1180

So, let me make a right triangle: I know that this angle right here (let me just draw the triangle out again--that doesn't look good;1191

this is more accurate)...this is that triangle here: this is 10, and I want to know either this or this.1208

Let's say that we are going to call that x.1219

Now, this is a right angle; we know that this is a 45-degree angle, because it is half the square; in squares, everything is regular.1223

So, to find the other sides of a 45-45-90 degree triangle, since we know that it is a special right triangle, we are going to use that shortcut.1236

If this is n, then this is n, and this is n√2; and in this case, I should label this n, because that is the side opposite the 45, which is n.1250

The side opposite this 45 is n, and then the side opposite the 90 is 10.1268

Here is the shortcut; I am given the 90-degree side, which is this right here, so I am going to make those equal to each other,1273

because this is n, and this is n√2, which is 10; so n√2 = 10.1281

Divide the √2 to both sides: I am going to solve for n; n = 10/√2...what do I do here?1292

Well, this square root is in the denominator, so I have to rationalize it; when I do that, this becomes 10√2/2; simplify this out; this becomes 5√2.1303

So again, what did I do? I took this...because I have this right here, the hypotenuse of this right triangle, I want to find this side right here.1324

I am going to use special right triangles, since this is a 45-45-90 degree triangle: n, n...the side opposite the 90 is n√2.1332

That is the side that I am given, so I am going to make that equal to n√2: n√2 = 10.1343

Solve for n by dividing the √2; let me rationalize the denominator, because I can't have a radical in the denominator.1350

So then, this becomes 10√2, over...√2 times √2 is just 2; simplify that out, and I get 5√2.1360

That means that n is 5√2; this side is 5√2; this side is 5√2.1370

Well, if this is 5√2, then what is this whole thing? We labeled that as s.1382

So, if this is 5√2, then this is 5√2; so you basically have to just multiply it by 2, because this is half of this whole side.1389

My side is 5√2 times 2, which is 10√2.1400

So, to find the area of the square, I am going to do 10√2 times 10√2, base times height (or side squared): 10√2, squared.1412

And then, I am going to use my calculator: this is 3.14 times 100, which is 314, minus 10√2 times 10√2;1427

that is 100 times 2; that is 200 (if you want, you can just double-check on your calculator).1445

This right here is (I'll just show you really quickly) 10√2 times 10√2.1452

10 times 10 is 100; √2 times √2 is times 2, so it is 100 times 2, which is 200.1464

Then, this is going to be 114; so the area of the gray is 114, because I took the area of the circle,1478

which was πr2, 314, and then I found the area of the square, which is 200, 10√2 times 10√2.1491

And then, I got 114; now, that is just the area of the gray; we are looking for the probability that it lands in the gray.1510

That is the area of the gray, over the area of the whole thing, which is the circle.1523

We take 114 over the area of the circle (where is the area of the circle?), which is 314; and that is the probability.1528

Now, we know that both of these numbers are even, so I can simplify it.1546

So then, if you were to cut this in half, this is going to be 57; if you cut this in half, this is going to be 157.1552

And that would be the probability, 57/157.1564

So again, the probability is going to be the area of the gray over the area of the whole thing, which is the circle.1573

The fourth example: we have a hexagon, and I am just going to go ahead and write that this is a regular hexagon with side length of 4 centimeters.1586

It is inscribed in a circle; what is the probability of a random point being in the hexagon?1599

"Inscribed": now, I don't have a diagram to show you, so I am going to have to draw it out.1606

"Inscribed" means that it is inside, so the hexagon is inside the circle; but all of the vertices of the hexagon are going to be on the circle.1611

They have to be intersecting; so let me first draw a circle, and the regular hexagon ("hexagon" means 6 sides).1627

I am going to try to draw this as regular as I possibly can, something like that, so it will look like it is inscribed...something like that.1641

What else do we have? Side length is 4 centimeters; what is the probability of a random point being in the hexagon?1666

OK, so then, again, we are giving a probability, so it is part over whole.1679

What is the part? The part will be the hexagon; inside the hexagon is the desired outcome--that is what we are looking for.1686

So, it is going to be the area of the hexagon, over...the whole thing is going to be the area of the circle.1693

Let's see, now: to find the area of this hexagon...remember: to find the area of a regular polygon,1711

if we were to take this hexagon and then break this up into triangles, we have 1, 2, 3, 4, 5, 6 triangles.1727

Each triangle is going to be 1/2 base times height; and then, we have 6 of them...times 6.1743

Now, if we take the base (the base is right here), and we multiply this base with this 6, isn't that the same thing as the perimeter?1756

The base, with the 6, is going to be the perimeter; the height, this right here, we call the apothem.1766

I am going to draw arrows to show that the base and the 6 together became the perimeter, and the height became the apothem.1785

1/2 just stayed as 1/2; this is the formula for the area of a regular polygon: it is 1/2 times the perimeter of the polygon, times the apothem.1792

The apothem is from the center, the segment going, not to a vertex, but to the center of the side; so it is perpendicular.1808

Now, we don't know what the apothem is, so I am going to have to look for it.1824

Now, remember: you always want to use right triangles, if you possibly can; we can, because the apothem is perpendicular to the side.1833

So, if I just maybe draw it bigger to show: this is the apothem.1843

If the whole side measures 4 (see how this is 4), then this half is going to be 2.1853

And then, I want to look for this angle measure, because I don't have this side.1863

If I have this side, then I can use the Pythagorean theorem, because then I have a2 + b2 = c2.1868

But I don't, so instead, I want to see: this is a circle; the whole thing, all the way around, is 360 degrees.1876

If I break this up into parts, this is 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.1886

I basically just look to see how much this triangle is from the whole 360; if the whole thing measures 360,1901

remember how we said that this is actually one of the 6 triangles; so 360 divided by 6 is 60.1913

Then, since this whole thing measures 60 degrees, what is this half right here?1927

This half is 30 degrees, so this is 30 and this is 60; and again, all I did was just...1932

I know that the whole thing, the full circle, measures 360; since I know that this right here is 60,1942

because I have 6 triangles, so it is like 6 triangles sharing 360 degrees;1950

then this angle right here is 60 degrees, which means that this half right here is 30.1956

A 30-60-90 triangle is a special right triangle; if this is n, the side opposite the 60 is n√3; the side opposite the 90 is 2n.1964

This is the special right triangle; what do I have--what am I given?1981

The side opposite the 30 is 2; so I am going to make those two equal to each other: n = 2.1988

That means that the side opposite the 60 is going to be 2√3; the side opposite the 90 is going to be 2 times n, which is 4.1999

That means that a, which is the side opposite my 60, is 2√3; isn't that my apothem, my a?2012

So, I know that that took a while; but it is just going over the area of a regular polygon.2020

It is 1/2 perimeter (which is 6 times 4, because there are 6 sides, and each side is 4...so perimeter is 24)...my apothem is 2√3.2033

And then, I can just cut this in half; so 24/2 is 12, times 2 is 24, √3.2053

To make that into a decimal, 24 times √3...we get 41.57 units squared...oh, we have centimeters, so this is centimeters squared.2065

And again, this is the area of the hexagon; so this is the hexagon, and then I want to find the area of the circle.2094

Now, if it were just the area of the hexagon that we were looking for, then this would be the answer.2110

But again, we are looking at probability: what is the probability of a random point being in the hexagon?2113

It is the area of the hexagon, over the area of the full circle.2124

So then, I look at it: here is the hexagon; here is the circle; the area is πr2.2131

π...do I know r?...r would be this length right here; this is the radius, because this is the center of the circle; this is a point on the circle.2144

From here to here...if this triangle is this triangle...what do we find about this side?2159

That side is opposite the 90, and that is 4; so this is 4 squared; this is 16π; 16 times π is 50.27 centimeters squared.2168

So then, hexagon over circle is 41.57, over 50.27; so let me just do that on a calculator: 41.57/50.27...and I get (so the probability is) 0.83.2199

Now, one thing to mention here: when you have a decimal, when you change your probability fraction into a decimal,2239

you have to make sure that it is less than 1, because, if you are looking at a part over the whole,2247

it is going to be a proper fraction; the part is going to be smaller that the whole.2257

If the whole is everything--it is the whole thing--well, then, the part can only be a fraction of it.2262

So, the only time you can get anything greater than this...2269

I'm sorry: the biggest number you can get for probability, when you change it to a decimal, is 1, because,2276

when you look at the fraction, it can just be the whole thing over the whole thing.2284

And when you have whole over whole, well, that is just going to equal 1, because it is the same number over itself.2289

So, make sure that your probability decimal is not greater than 1, unless you are talking about the whole thing.2296

Then, it is going to be 100%, all of it, which is 1; but otherwise, if the part is smaller than the whole, then your decimal has to be less than 1.2304

That is it for this lesson; thank you for watching Educator.com.2318

Related Books

Related Books

Educator®

Please sign in to participate in this lecture discussion.

Resetting Your Password?
or
Still having trouble? Contact us
OR

Start Learning Now

Our free lessons will get you started (Adobe Flash® required).
 Get immediate access to our entire library.

Membership Overview

  • Available 24/7. Unlimited Access to Our Entire Library.
  • Search and jump to exactly what you want to learn.
  • *Ask questions and get answers from the community and our teachers!
  • Practice questions with step-by-step solutions.
  • Download lecture slides for taking notes.
  • Track your course viewing progress.
  • Accessible anytime, anywhere with our Android and iOS apps.