Connecting...

This is a quick preview of the lesson. For full access, please Log In or Sign up.
For more information, please see full course syllabus of Geometry
For more information, please see full course syllabus of Geometry
Geometry Secants, Tangents, & Angle Measures
Lecture Description
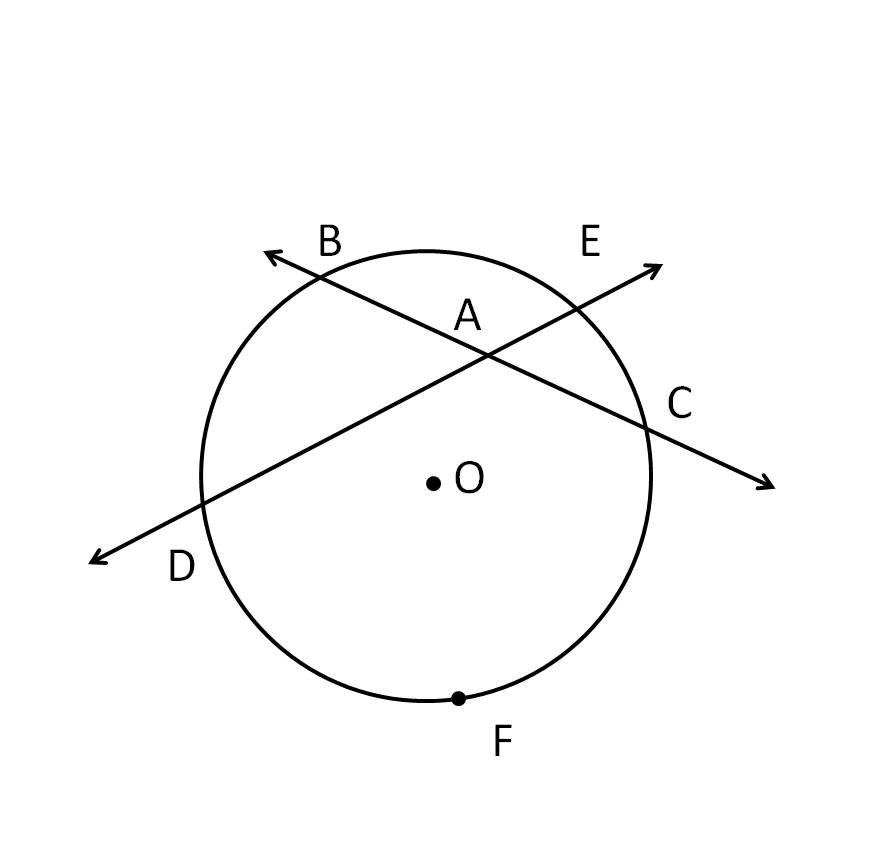
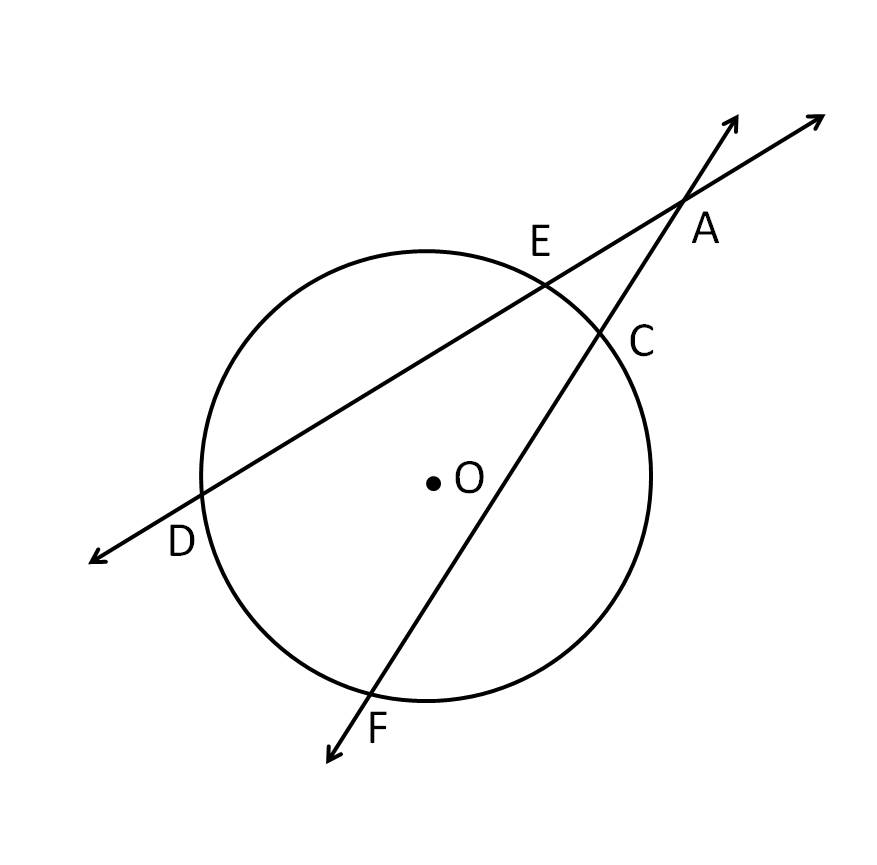
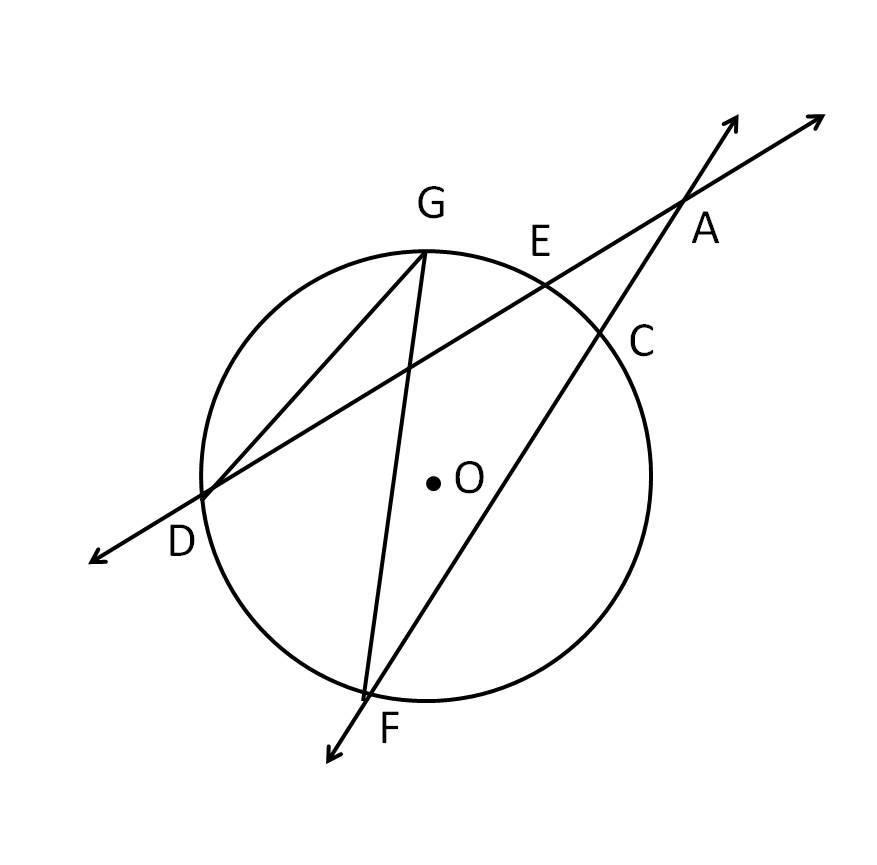
In this lesson we are going to talk about secants, tangents, and angle measures. We have already learned that a tangent intersects a circle in exactly one point. On the other hand, a secant is a line that intersects a circle in exactly two points of a circle. There's an important theorem we are going to go over and it tells us that if a secant and a tangent intersect at the point of tangency, then the measure of each angle formed is one-half the measure of its intercepted arc. This theorem will help you solve many geometry problems. You'll also see what happens when two secants intersect in the interior of a circle, as well as in the exterior of a circle.
Bookmark & Share
Embed
Share this knowledge with your friends!
Copy & Paste this embed code into your website’s HTML
Please ensure that your website editor is in text mode when you paste the code.(In Wordpress, the mode button is on the top right corner.)
×
Since this lesson is not free, only the preview will appear on your website.
- - Allow users to view the embedded video in full-size.
Next Lecture
Previous Lecture










































 Answer Engine
Answer Engine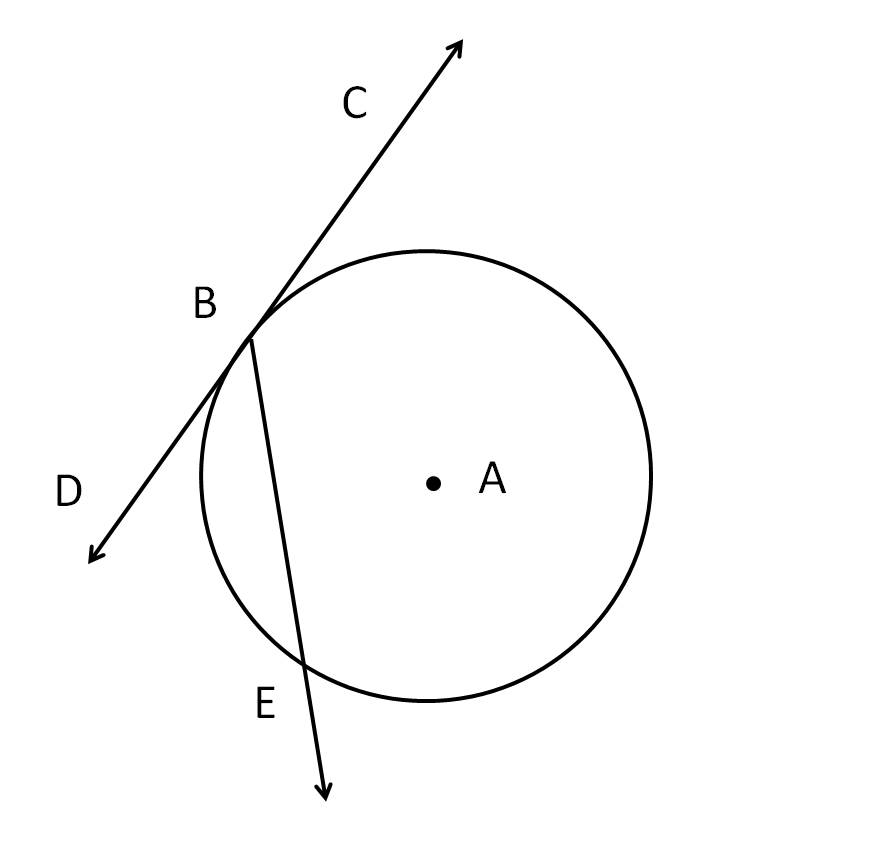






1 answer
Last reply by: Denise Bermudez
Thu Mar 12, 2015 5:44 PM
Post by Denise Bermudez on March 12, 2015
hi!
I dont understand why in minute 26:13 you multiplied both by three. What answer would you have gotten if you didnt do that multiplication process to both sides. I also dont understand if you multiplied both sides then why do you still end up with a 120 and 30 becomes a 60?
thanks loved all of your lessons!